题目内容
对任意的实数x,不等式x+|x-1|>m恒成立,则实数m的取值范围是分析:令f(x)=x+|x-1|,依题意,只需求得f(x)min即可求得m的取值范围.
解答:解:令f(x)=x+|x-1|=
,
∴(x+|x-1|)min=1,
∴m<1.
故答案为:m<1.
|
∴(x+|x-1|)min=1,
∴m<1.
故答案为:m<1.
点评:本题考查函数恒成立问题,求得f(x)min是关键,属于中档题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 则f1(x)∈M;
则f1(x)∈M;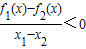 ;
;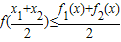 .
.