题目内容
棱长均为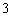 三棱锥
三棱锥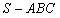 ,若空间一点
,若空间一点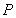 满足
满足
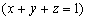 则
则 的最小值为( )
的最小值为( )
A、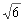 B、
B、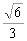 C、
C、 D、
D、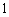
【答案】
A
【解析】
试题分析:根据空间向量基本定理知,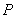 与
与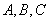 共面,则
共面,则 的最小值为三棱锥的高,所以
的最小值为三棱锥的高,所以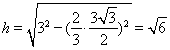 ,故选A.
,故选A.
考点:1.空间向量基本定理;2.正四面体的应用.

练习册系列答案
相关题目
题目内容
棱长均为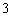 三棱锥
三棱锥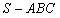 ,若空间一点
,若空间一点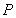 满足
满足
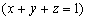 则
则 的最小值为( )
的最小值为( )
A、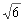 B、
B、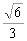 C、
C、 D、
D、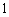
A
【解析】
试题分析:根据空间向量基本定理知,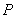 与
与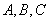 共面,则
共面,则 的最小值为三棱锥的高,所以
的最小值为三棱锥的高,所以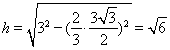 ,故选A.
,故选A.
考点:1.空间向量基本定理;2.正四面体的应用.
