题目内容
在△ABC,A=60°,BC=2,AC=2
| ||
| 3 |
分析:先个根据正弦定理求出sinB,进而求出B.根据A,B判断△ABC的形状.
解答:解:根据正弦定理
=
∴sinB=
=
=
∴B=30°或150°
∵BC>AC
∴sinB<sinA
∴B=30°
∴A+B=90°
∴△ABC为直角三角形.
故答案为直角三角形.
| AC |
| sinB |
| BC |
| sinA |
∴sinB=
| AC•sinA |
| BC |
| ||||||||
| 2 |
| 1 |
| 2 |
∴B=30°或150°
∵BC>AC
∴sinB<sinA
∴B=30°
∴A+B=90°
∴△ABC为直角三角形.
故答案为直角三角形.
点评:本题主要考查了正弦定理的应用.属基础题.

练习册系列答案
相关题目

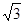 -2 C.
-2 C. -1)
-1)