题目内容
在直三棱柱ABC—A1B1C1中,AB=AC=AA1=3,BC=2,D为BC的中点,点E为棱CC1上一点.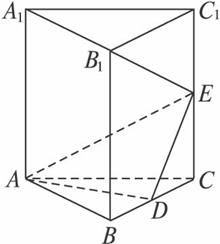
(1)当![]() 的值为多少时,能使B1E⊥平面ADE?请你给出证明;
的值为多少时,能使B1E⊥平面ADE?请你给出证明;
(2)当![]() =2时,求四面体ACDE的内切球的半径.
=2时,求四面体ACDE的内切球的半径.
解:∵ABC—A1B1C1是直棱柱,且AB=AC=AA1=3,BC=2,D是BC的中点.
∴AD⊥BC,则AD⊥平面BCC1B1,∴AD⊥B1E.

(1)若B1E⊥平面ADE,则B1E⊥DE,
∴△B1EC1∽△EDC,
∴![]() ,设C1E=x,则
,设C1E=x,则![]() ,∴x=1或x=2;
,∴x=1或x=2;
∴![]() 或
或![]() =2时,B1E⊥平面ADE.
=2时,B1E⊥平面ADE.
(2)依题意,EC=1,设内切球半径为r.
∵![]() S△ADC·EC=
S△ADC·EC=![]() r(S△ADC+S△DCE+S△ACE+S△ADE),
r(S△ADC+S△DCE+S△ACE+S△ADE),
∴![]() =r(
=r(![]() +1+3+
+1+3+![]() ×
×![]() )=r(
)=r(![]() +8),
+8),
∴r=![]() ,∴
,∴![]() =2时,四面体ACDE的内切球半径为
=2时,四面体ACDE的内切球半径为![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
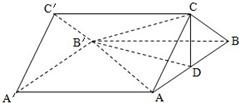 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点. (2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a,
(2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a, 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数). 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,