题目内容
在△ABC中，a，b，c分别是角A、B、C的对边，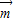
=（2b-c，cosC），
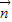=（a，cosA），且
∥
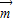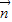．（1）求角A的大小；
（2）求
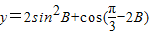的值域．
【答案】分析：（1）用向量的共线的充要条件及三角形中的正弦定理求得角A．
（2）用三角函数的二倍角公式化简函数，再利用正弦函数的图象求出范围．
解答：解：（1）由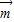
∥
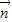得（2b-c）•cosA-acosC=0，
由正弦定理得2sinBcosA-sinCcosA-sinAcosC=0，2sinBcosA-sin（A+C）=0，
∴2sinBcosA-sinB=0，
∵
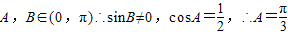
（2）
，=
．
=
，
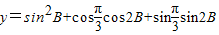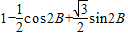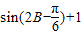由（1）得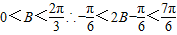
，
∴
∴
．
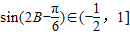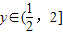答：角A的大小；函数的值域为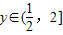
点评：本题考查向量与三角函数相结合的综合问题，是高考中常出现的形式．
（2）用三角函数的二倍角公式化简函数，再利用正弦函数的图象求出范围．
解答：解：（1）由
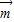∥得（2b-c）•cosA-acosC=0，由正弦定理得2sinBcosA-sinCcosA-sinAcosC=0，2sinBcosA-sin（A+C）=0，
∴2sinBcosA-sinB=0，
∵
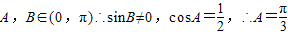
（2）
，=．=
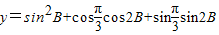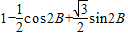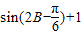，由（1）得
，∴
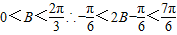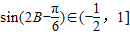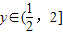∴．答：角A的大小；函数的值域为
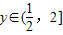
点评：本题考查向量与三角函数相结合的综合问题，是高考中常出现的形式．
练习册系列答案
相关题目
在△ABC中，∠A、∠B、∠C所对的边长分别是a、b、c．满足2acosC+ccosA=b．则sinA+sinB的最大值是（ ）
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|