题目内容
抛物线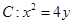 ,直线
,直线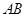 过抛物线
过抛物线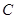 的焦点
的焦点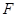 ,交
,交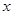 轴于点
轴于点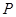 .
.
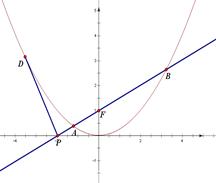
(1)求证: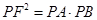 ;
;
(2)过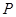 作抛物线
作抛物线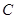 的切线,切点为
的切线,切点为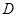 (异于原点),
(异于原点),
(ⅰ)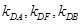 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;
(ⅱ)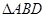 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.
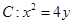 ,直线
,直线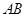 过抛物线
过抛物线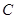 的焦点
的焦点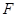 ,交
,交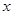 轴于点
轴于点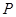 .
.
(1)求证:
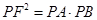 ;
;(2)过
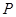 作抛物线
作抛物线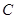 的切线,切点为
的切线,切点为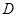 (异于原点),
(异于原点),(ⅰ)
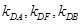 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;(ⅱ)
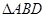 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.(1) 即证 (2) 能 抛物线
(2) 能 抛物线
 (2) 能 抛物线
(2) 能 抛物线
试题分析:(1)由于点F的坐标已知,所以可假设直线AB的方程(依题意可得直线AB的斜率存在).写出点P的坐标,联立直线方程与抛物线方程消去y,即可得到一个关于x的一元二次方程,写出韦达定理,再根据欲证
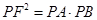 转化为点的坐标关系.
转化为点的坐标关系.(2)(ⅰ)根据提议分别写出
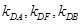 ,结合韦达定理验证
,结合韦达定理验证 是否成立.
是否成立.(ⅱ)由三角形重心的坐标公式,结合韦达定理,消去参数k即可得到重心的轨迹.
(1)因为
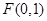 ,所以假设直线AB为
,所以假设直线AB为 ,
, ,所以点
,所以点 .联立
.联立 可得,
可得, ,所以
,所以 .因为
.因为 ,
,
 .所以
.所以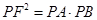 .
.(2)(ⅰ)设
 ,
, 的导数为
的导数为 .所以可得
.所以可得 ,即可得
,即可得 .即得
.即得 .
. .
.

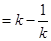 .所以可得
.所以可得 即
即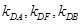 是否恒成等差数列.
是否恒成等差数列.(ⅱ)因为
 重心的坐标为
重心的坐标为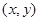 由题意可得
由题意可得 .即
.即 ,
,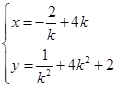 消去k可得
消去k可得 .
.
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 (
( )是曲线
)是曲线 上的点,
上的点, ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足 ,
, ,
, .
. (
( )是常数数列;
)是常数数列; 的取值集合
的取值集合 ,使
,使 时,数列
时,数列 (
( 是各项为不同的正数的等差数列,
是各项为不同的正数的等差数列, 成等差数列,又
成等差数列,又 .
. 为等比数列;
为等比数列; ,求数列
,求数列 为数列
为数列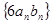 的前
的前 项和,求
项和,求 满足
满足 .
. 项和
项和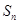 ;
; 成等比数列,求
成等比数列,求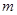 的值.
的值.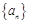 中,
中,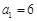 ,且
,且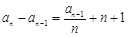 (
(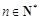 ,
,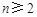 ),则这个数列的
),则这个数列的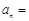 ______________.
______________. 为正项等比数列,
为正项等比数列, ,
, ,
, 为等差数列
为等差数列 的前
的前
 ,
, .
. ,求
,求 .
.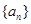 中,
中,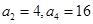 .
.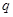 ;
;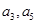 分别为等差数列
分别为等差数列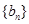 的第3项和第5项,求数列
的第3项和第5项,求数列 ,三边长a,b,c成等差数列,且ac=6,则b的值是( )
,三边长a,b,c成等差数列,且ac=6,则b的值是( )



 为等差数列
为等差数列 的前
的前 项和,
项和, ,则
,则 =
=

