题目内容
如图,在底面是正方形的四棱锥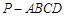 中,
中,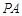
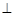 面
面 ,
,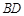 交
交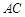 于点
于点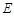 ,
,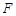 是
是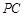 中点,
中点,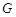 为
为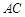 上一动点.
上一动点.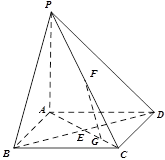
(1)求证: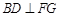 ;
;
(1)确定点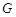 在线段
在线段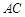 上的位置,使
上的位置,使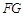 //平面
//平面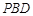 ,并说明理由.
,并说明理由.
(3)如果PA=AB=2,求三棱锥B-CDF的体积
⑴详见解析;⑵当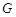 为
为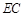 中点时,
中点时,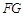 //平面
//平面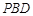 ;(3)三棱锥B-CDF的体积为
;(3)三棱锥B-CDF的体积为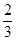 .
.
解析试题分析:⑴证空间两直线垂直的常用方法是通过线面垂直来证明,本题中,由于直线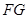 在平面
在平面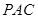 内,所以考虑证明
内,所以考虑证明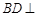 平面
平面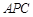 .⑵注意平面
.⑵注意平面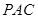 与平面
与平面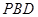 相交于
相交于 ,而直线
,而直线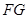 在平面
在平面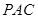 内,故只需
内,故只需 即可,而这又只需
即可,而这又只需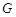 为
为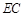 中点即可.(3)求三棱锥B-CDF的体积中转化为求三棱锥F-BCD的体积,这样底面面积与高都很易求得.
中点即可.(3)求三棱锥B-CDF的体积中转化为求三棱锥F-BCD的体积,这样底面面积与高都很易求得.
试题解析:⑴∵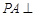 面
面 ,四边形
,四边形 是正方形,
是正方形,
其对角线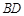 、
、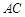 交于点
交于点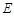 ,
,
∴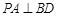 ,
, .2分
.2分
∴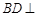 平面
平面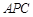 , 3分
, 3分
∵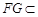 平面
平面 ,
,
∴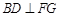 4分
4分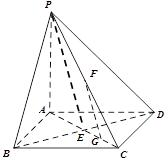
⑵当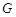 为
为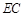 中点,即
中点,即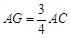 时,
时,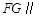 /平面
/平面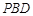 , 5分
, 5分
理由如下:
连结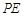 ,由
,由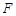 为
为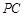 中点,
中点,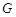 为
为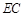 中点,知
中点,知 6分
6分
而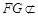 平面
平面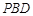 ,
,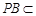 平面
平面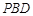 ,
,
故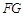 //平面
//平面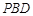 . 8分
. 8分
(3)三棱锥B-CDF的体积为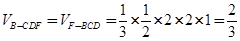 .12分
.12分
考点:1、空间直线与平面的关系;2、三棱锥的体积.

练习册系列答案
相关题目
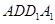 和三棱锥
和三棱锥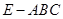 组合而成,点
组合而成,点 、
、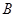 、
、 在圆
在圆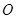 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中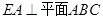 ,
,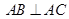 ,
,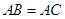 ,
,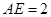 .
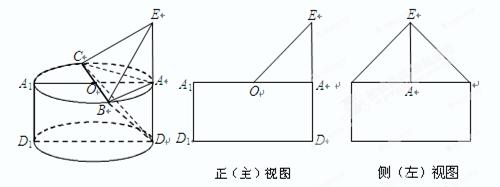
.
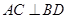 ;
;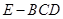 的体积.
的体积.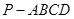 中,底面
中,底面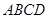 是菱形,
是菱形,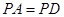 ,
,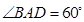 ,
,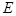 是
是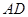 的中点,点
的中点,点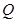 在侧棱
在侧棱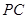 上.
上.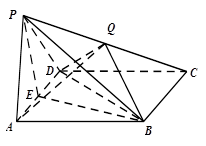
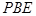 ;
; //平面
//平面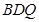 ;
;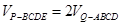 ,试求
,试求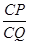 的值.
的值.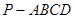 中,
中,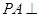 平面
平面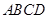 ,底面
,底面 是平行四边形,
是平行四边形,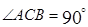 ,
,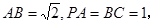
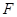 是
是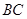 的中点
的中点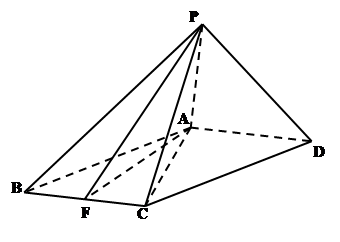
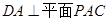
 上确定一点
上确定一点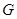 ,使
,使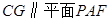 ,求三棱锥
,求三棱锥 的体积.
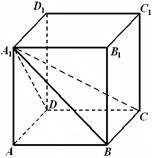
的体积. 的棱长为
的棱长为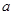 .
.
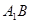 与
与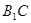 所成角的大小;
所成角的大小;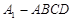 的体积.
的体积.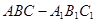 的三视图如图所示,且
的三视图如图所示,且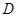 是
是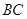 的中点.
的中点.
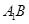 ∥平面
∥平面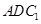 ;
;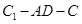 的余弦值;
的余弦值;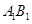 上是否存在点
上是否存在点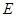 ,使
,使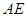 与
与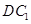 成
成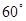 角?若存在,确定
角?若存在,确定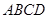 中
中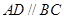 ,
,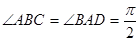 ,
,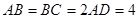 ,
,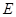 、
、 分别是
分别是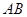 、
、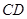 上的点,
上的点,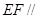
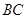 ,
,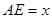 .沿
.沿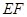 将梯形
将梯形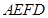 翻折,使平面
翻折,使平面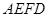 ⊥平面
⊥平面 (如图).
(如图).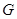 是
是
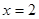 时,求证:
时,求证: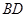 ⊥
⊥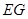 ;
; 变化时,求三棱锥
变化时,求三棱锥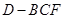 体积的最大值.
体积的最大值. 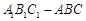 中,侧面
中,侧面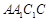
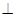 底面ABC,底面ABC是边长为2的等边三角形,侧面
底面ABC,底面ABC是边长为2的等边三角形,侧面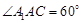 ,E、F分别是
,E、F分别是 、AB的中点.
、AB的中点.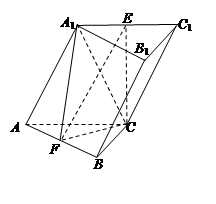
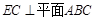 ;
;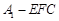 的体积.
的体积.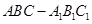 中,
中,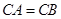 ,
,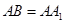 ,
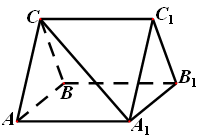
,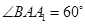 。
。
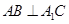 ;
;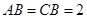 ,
,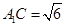 ,求三棱柱
,求三棱柱