题目内容
已知曲线![]() 过
过![]() 上的点
上的点![]() 作曲线
作曲线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,再过
,再过![]() 作
作![]() 轴的平行线交曲线C于点
轴的平行线交曲线C于点![]() ,再过
,再过![]() 作曲线C的切线
作曲线C的切线![]() 交
交![]() 轴于点
轴于点![]() ,再过
,再过![]() 作
作![]() 轴的平行线交曲线C于点
轴的平行线交曲线C于点![]() ,…,依次作下去,记点
,…,依次作下去,记点![]() 的横坐标为
的横坐标为![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() .
.
解:(I)∵![]() . ∴曲线
. ∴曲线![]() 在点
在点![]() 处的切线ln的斜率为
处的切线ln的斜率为![]() .
.
∴切线ln的方程为![]() .
.
令![]() 得
得 ![]() ,
,
∴![]() .
.
依题意点![]() 在直线
在直线![]() 上,
上,
∴![]() 又
又![]() .
.
∴数列![]() 是1为首项,
是1为首项,![]() 为公比的等比数列.
为公比的等比数列.
∴![]() .
.
(Ⅱ)由已知![]() .
.
∴![]() . ①
. ①
![]() . ②
. ②
①―②得
![]()
![]()
 .
.
∴![]()
又![]() 时,
时,![]() .
.
又当![]() 时,
时,![]() .
.
∴![]() .
.
∴当![]() 时,
时,![]() .
.
∴![]() ∴
∴![]() .
.
综上![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
,  是平面上一动点,
是平面上一动点,  上的射影为点
上的射影为点 ,且满足
,且满足
 的方程;
的方程;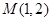 作曲线
作曲线 , 设
, 设 , 当
, 当 时,证明直线
时,证明直线 恒过定点,并求出该定点坐标.
恒过定点,并求出该定点坐标. ,
,  是平面上一动点,
是平面上一动点,  上的射影为点
上的射影为点 ,且满足
,且满足
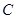 的方程;
的方程; 作曲线
作曲线 , 设
, 设 , 当
, 当 时,证明直线
时,证明直线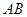 恒过定点,并求出该定点坐标。
恒过定点,并求出该定点坐标。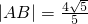 ,动点P满足
,动点P满足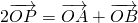 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C. 交于M、N两点,求证:
交于M、N两点,求证: 为定值.
为定值.