题目内容
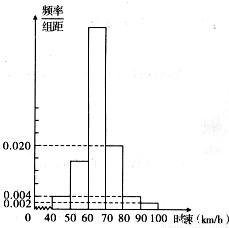
 为了减少交通事故,某市在不同路段对机动车时速有不同的限制.2011年6月9日,在限速为70km/h的某一路段上,流动测速车对经过该路段的100辆机动车进行测速,如图是所测100辆机动车时速的频率分布直方图.
为了减少交通事故,某市在不同路段对机动车时速有不同的限制.2011年6月9日,在限速为70km/h的某一路段上,流动测速车对经过该路段的100辆机动车进行测速,如图是所测100辆机动车时速的频率分布直方图.
(Ⅰ)写出被测100辆机动车时速的众数,并估计其中任意一辆车超速的概率;
(Ⅱ)求这100辆车中超速的车辆数;若在这些超速车辆中采用分层抽样的方法抽取9辆,计算每一时速段应抽取的车辆数.
(Ⅲ)从超速的车辆中随机抽取1辆,让该车的驾驶员参加《道路交通安全法》知识竞赛,求该车时速在(80,90]的概率.
解:(I)由频率分布直方图可得,直方图中最高的矩形的底边的中点即为众数,
故机动车时速的众数为65,
车速在(70,80]内的频率为1-(0.06+0.018+0.004+0.002+0.004)×10=0.12.
则估计其中任意一辆车超速的概率为0.12+(0.004+0.002)×10=0.18.
(II)超速的车辆数为:0.12+0.004×10+0.002×10)×100=18,
在车速为(70,80]、(80,90]和(90.100]内抽取的车辆数之比为:0.12:0.004:0.002=6:2:1,
故在车速为(70,80]、(80,90]和(90.100]内抽取的车辆数分别为6、2、1.
(III)从超速的9辆车辆中随机抽取1辆,该车时速在(80,90]的有2辆,
故概率为:P= .
.
分析:(I)选出直方图中最高的矩形求出其底边的中点即为众数;
(II)由频率分布图可以看出,超速的车辆数,在车速为(70,80]、(80,90]和(90.100]内抽取的车辆数之比,从而得出在车速为(70,80]、(80,90]和(90.100]内抽取的车辆数.
(Ⅲ)从超速的9辆车辆中随机抽取1辆,该车时速在(80,90]的有2辆,根据概率计算公式求解即可.
点评:解决此类问题的关键是熟悉频率分布直方图并且利用直方图计算平均数、众数、中位数;熟练的利用分层抽样抽取样本.
故机动车时速的众数为65,
车速在(70,80]内的频率为1-(0.06+0.018+0.004+0.002+0.004)×10=0.12.
则估计其中任意一辆车超速的概率为0.12+(0.004+0.002)×10=0.18.
(II)超速的车辆数为:0.12+0.004×10+0.002×10)×100=18,
在车速为(70,80]、(80,90]和(90.100]内抽取的车辆数之比为:0.12:0.004:0.002=6:2:1,
故在车速为(70,80]、(80,90]和(90.100]内抽取的车辆数分别为6、2、1.
(III)从超速的9辆车辆中随机抽取1辆,该车时速在(80,90]的有2辆,
故概率为:P=
 .
.分析:(I)选出直方图中最高的矩形求出其底边的中点即为众数;
(II)由频率分布图可以看出,超速的车辆数,在车速为(70,80]、(80,90]和(90.100]内抽取的车辆数之比,从而得出在车速为(70,80]、(80,90]和(90.100]内抽取的车辆数.
(Ⅲ)从超速的9辆车辆中随机抽取1辆,该车时速在(80,90]的有2辆,根据概率计算公式求解即可.
点评:解决此类问题的关键是熟悉频率分布直方图并且利用直方图计算平均数、众数、中位数;熟练的利用分层抽样抽取样本.

练习册系列答案
相关题目
 为了减少交通事故,某市在不同路段对机动车时速有不同的限制.2011年6月9日,在限速为70km/h的某一路段上,流动测速车对经过该路段的100辆机动车进行测速,如图是所测100辆机动车时速的频率分布直方图.
为了减少交通事故,某市在不同路段对机动车时速有不同的限制.2011年6月9日,在限速为70km/h的某一路段上,流动测速车对经过该路段的100辆机动车进行测速,如图是所测100辆机动车时速的频率分布直方图. 为了减少交通事故,某市在不同路段对机动车时速有不同的限制.2011年6月9日,在限速为70km/h的某一路段上,流动测速车对经过该路段的100辆机动车进行测速,如图是所测100辆机动车时速的频率分布直方图.
为了减少交通事故,某市在不同路段对机动车时速有不同的限制.2011年6月9日,在限速为70km/h的某一路段上,流动测速车对经过该路段的100辆机动车进行测速,如图是所测100辆机动车时速的频率分布直方图.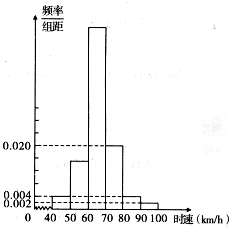 为了减少交通事故,某市在不同路段对机动车时速有不同的限制.2011年6月9日,在限速为70km/h的某一路段上,流动测速车对经过该路段的100辆机动车进行测速,如图是所测100辆机动车时速的频率分布直方图.
为了减少交通事故,某市在不同路段对机动车时速有不同的限制.2011年6月9日,在限速为70km/h的某一路段上,流动测速车对经过该路段的100辆机动车进行测速,如图是所测100辆机动车时速的频率分布直方图.