题目内容
(本题10分)已知函数 是奇
是奇
函数,当x>0时, 有最小值2,且f (1)
有最小值2,且f (1) .
.
(Ⅰ)试求函数 的解析式;
的解析式;
(Ⅱ)函数 图象上是否存在关于点(1,0)对称的两点?若存在,求出点的坐标;若不存在,说明理由.
图象上是否存在关于点(1,0)对称的两点?若存在,求出点的坐标;若不存在,说明理由.
 是奇
是奇函数,当x>0时,
 有最小值2,且f (1)
有最小值2,且f (1) .
.(Ⅰ)试求函数
 的解析式;
的解析式;(Ⅱ)函数
 图象上是否存在关于点(1,0)对称的两点?若存在,求出点的坐标;若不存在,说明理由.
图象上是否存在关于点(1,0)对称的两点?若存在,求出点的坐标;若不存在,说明理由.解:(Ⅰ)∵f(x)是奇函数 ∴f(―x) =―f(x)
即
 ……………………1分
……………………1分

当且仅当 时等号成立.则
时等号成立.则 ……2分
……2分
由 得
得 ,即
,即 ,
,
 ,解得
,解得 ;
;
又 ,
,
 …………………………
………………………… …………………5分
…………………5分
(Ⅱ)设存在一点(x0,y0)在y="f" (x)图象上,
则关于(1,0)的对称点( ,―y0)也在y ="f" (x)图象上, …………6分
,―y0)也在y ="f" (x)图象上, …………6分
则 解得:
解得: 或
或
∴函数f (x)图象上存在两点 和
和 关于点(1,0)对
关于点(1,0)对 称. …………………………………10分
称. …………………………………10分
即

 ……………………1分
……………………1分
当且仅当
 时等号成立.则
时等号成立.则 ……2分
……2分由
 得
得 ,即
,即 ,
, ,解得
,解得 ;
;又
 ,
,
 …………………………
………………………… …………………5分
…………………5分(Ⅱ)设存在一点(x0,y0)在y="f" (x)图象上,
则关于(1,0)的对称点(
 ,―y0)也在y ="f" (x)图象上, …………6分
,―y0)也在y ="f" (x)图象上, …………6分则
 解得:
解得: 或
或
∴函数f (x)图象上存在两点
 和
和 关于点(1,0)对
关于点(1,0)对 称. …………………………………10分
称. …………………………………10分略

练习册系列答案
相关题目
 的图象大致是
的图象大致是 
 为定义域和值域的函数的是( )
为定义域和值域的函数的是( )
 的图象是
的图象是
 的图象是
的图象是
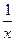 ∣-∣x-
∣-∣x- 的图像可能是 ( )
的图像可能是 ( )
 在闭区间
在闭区间 上的最大值记为
上的最大值记为
 ,
,  恒成立,求
恒成立,求 的取值范围.
的取值范围.
 或
或 行驶,在全程中,甲的时间速度关系如图甲,乙的路程速度关系如图乙,那么下列说法正确的是
行驶,在全程中,甲的时间速度关系如图甲,乙的路程速度关系如图乙,那么下列说法正确的是

 达B地
达B地