题目内容
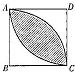如图，设F是图中边长为1的正方形区域，E是分别以B，D为圆心，1为半径的圆的公共部分，向F中随机投一点，则该点落入E中的概率为
- A.
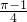
- B.
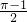
- C.
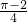
- D.
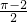
D
分析：由题意知本题是一个几何概型，试验发生包含的所有事件是矩形面积S=1×2，而空白区域可以看作是由二部分组成，每一部分是由边长为1的正方形面积减去半径为1的四分之一圆的面积得到，最后利用几何概型的概率公式解之即可．
解答：由题意知本题是一个几何概型，
∵试验发生包含的所有事件是矩形面积S=1×2=2，
空白区域的面积是2（1-
π）=2-
π，
则区域E的面积为1-（2-π）=
-1
∴由几何概型公式得到P=
=，
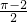故选D．
点评：本题主要考查了几何概型，解题的关键求阴影部分的面积，同时考查了计算能力，属于中档题．
分析：由题意知本题是一个几何概型，试验发生包含的所有事件是矩形面积S=1×2，而空白区域可以看作是由二部分组成，每一部分是由边长为1的正方形面积减去半径为1的四分之一圆的面积得到，最后利用几何概型的概率公式解之即可．
解答：由题意知本题是一个几何概型，
∵试验发生包含的所有事件是矩形面积S=1×2=2，
空白区域的面积是2（1-
π）=2-π，则区域E的面积为1-（2-
π）=-1∴由几何概型公式得到P=
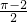=，故选D．
点评：本题主要考查了几何概型，解题的关键求阴影部分的面积，同时考查了计算能力，属于中档题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
如图，P-ABC是底面边长为1的正三棱锥，D、E、F分别为棱长PA、PB、PC上的点，截面DEF∥底面ABC，且棱台DEF-ABC与棱锥P-ABC的棱长和相等．（棱长和是指多面体中所有棱的长度之和）
如图，设F是图中边长为1的正方形区域，E是分别以B，D为圆心，1为半径的圆的公共部分，向F中随机投一点，则该点落入E中的概率为（ ）
PA，求二面角D-BC-A的大小；（结果用反三角函数值表示）
求二面角D-BC-A的大小；（结果用反三角函数值表示）