题目内容
已知f(x),g(x)都是定义在R上的函数,且f(x)=g(x)ax(a>0且a≠1)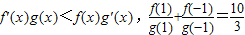 ,则a的值为 .
,则a的值为 .
【答案】分析:先将函数f(x)=g(x)ax转化为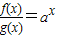 ,利用导数条件判断指数函数的单调性,然后利用条件求值.
,利用导数条件判断指数函数的单调性,然后利用条件求值.
解答:解:因为f(x)=g(x)ax,得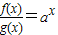 ,设
,设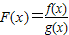 ,则
,则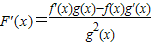 ,
,
所以F'(x)<0,即函数F(x)单调递减,所以0<a<1.
由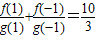 ,得
,得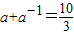 ,即
,即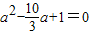 ,解得a=3(舍得)或a=
,解得a=3(舍得)或a= .
.
故答案为: .
.
点评:本题的考点是利用导数研究函数的单调性,将函数转化为商的形式,然后求导数判断导数符号,从而确定a的大小是解决本题的关键.
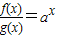 ,利用导数条件判断指数函数的单调性,然后利用条件求值.
,利用导数条件判断指数函数的单调性,然后利用条件求值.解答:解:因为f(x)=g(x)ax,得
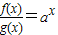 ,设
,设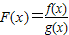 ,则
,则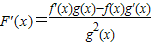 ,
,所以F'(x)<0,即函数F(x)单调递减,所以0<a<1.
由
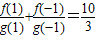 ,得
,得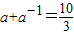 ,即
,即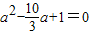 ,解得a=3(舍得)或a=
,解得a=3(舍得)或a= .
.故答案为:
 .
.点评:本题的考点是利用导数研究函数的单调性,将函数转化为商的形式,然后求导数判断导数符号,从而确定a的大小是解决本题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目