题目内容
 (2013•丰台区一模)如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.
(2013•丰台区一模)如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.(Ⅰ)求证:AC⊥PD;
(Ⅱ)在线段PA上,是否存在点E,使BE∥平面PCD?若存在,求
| PE | PA |
分析:(I)利用面面垂直的性质定理即可证明;
(II)线段PA上,存在点E,使BE∥平面PCD.在△PAD中,分别取PA、PD靠近点P的三等分点E、F,连接EF.由平行线分线段成比例定理在三角形中的应用,即可得到EF∥AD,EF=
AD=1.利用已知条件即可得到EF
BC,得到四边形BCFE为平行四边形,再利用线面平行的判定定理即可证明.
(II)线段PA上,存在点E,使BE∥平面PCD.在△PAD中,分别取PA、PD靠近点P的三等分点E、F,连接EF.由平行线分线段成比例定理在三角形中的应用,即可得到EF∥AD,EF=
| 1 |
| 3 |
| ∥ |
. |
解答:(Ⅰ)证明:∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,AC⊥CD,AC?平面ABCD,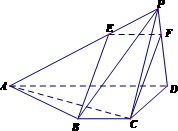
∴AC⊥平面PCD,
∵PD?平面PCD,
∴AC⊥PD.
(Ⅱ)线段PA上,存在点E,使BE∥平面PCD.下面给出证明:
∵AD=3,
∴在△PAD中,分别取PA、PD靠近点P的三等分点E、F,连接EF.
∵
=
=
,∴EF∥AD,EF=
AD=1.
又∵BC∥AD,∴BC∥EF,且BC=EF,
∴四边形BCFE是平行四边形,
∴BE∥CF,BE?平面PCD,CF?平面PCD,
∴BE∥平面PCD.

∴AC⊥平面PCD,
∵PD?平面PCD,
∴AC⊥PD.
(Ⅱ)线段PA上,存在点E,使BE∥平面PCD.下面给出证明:
∵AD=3,
∴在△PAD中,分别取PA、PD靠近点P的三等分点E、F,连接EF.
∵
| PE |
| PA |
| PF |
| PD |
| 1 |
| 3 |
| 1 |
| 3 |
又∵BC∥AD,∴BC∥EF,且BC=EF,
∴四边形BCFE是平行四边形,
∴BE∥CF,BE?平面PCD,CF?平面PCD,
∴BE∥平面PCD.
点评:熟练掌握面面垂直的性质定理、平行线分线段成比例定理在三角形中的应用、平行四边形的判定和性质定理、线面平行的判定定理是解题的关键.

练习册系列答案
相关题目
 (2013•丰台区一模)执行右边的程序框图所得的结果是( )
(2013•丰台区一模)执行右边的程序框图所得的结果是( )