题目内容
已知函数f(x)=log2 ,(x∈(-∞,-
,(x∈(-∞,- )∪(
)∪( ,+∞))
,+∞))
(1)判断函数f(x)的奇偶性,并说明理由;
(2)判断函数f(x)在区间( ,+∞)上的单调性.
,+∞)上的单调性.
解:(1)函数f(x)是奇函数.证明如下
证明:由题意可得函数的定义域关于原点对称
因为f(-x)=log2 =log2
=log2 =log2(
=log2( )-1=-f(x),
)-1=-f(x),
所以函数f(x)是奇函数.
(2)f(x)在区间( ,+∞)上的单调递减,证明如下
,+∞)上的单调递减,证明如下
证明:令g(x)= =
= =
=
设 ,则g(x1)-g(x2)=
,则g(x1)-g(x2)=

= =
=
∵ ,则x1-x2<0,
,则x1-x2<0,
∴即g(x1)<g(x2)
∴g(x)在(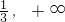 )上单调递减
)上单调递减
由于y=log2g(x)在(0,+∞)单调递增,由复合函数的单调性可知y= 在(
在(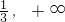 )单调递减
)单调递减
分析:(1)由f(-x)=log2 =log2
=log2 =log2(
=log2( )-1=-f(x),可得
)-1=-f(x),可得
(2)令g(x)= =
= =
= ,只要利用单调性的定义先检验函数g(x)在(
,只要利用单调性的定义先检验函数g(x)在(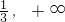 )上单调性,结合y=log2g(x)在(0,+∞)单调性及复合函数的单调性可判断
)上单调性,结合y=log2g(x)在(0,+∞)单调性及复合函数的单调性可判断
点评:本题主要考查了奇偶函数的定义、函数单调性的定义在判断函数的奇偶性、单调性中中的应用,解题的关键是熟练掌握基本定义、基本方法
证明:由题意可得函数的定义域关于原点对称
因为f(-x)=log2
 =log2
=log2 =log2(
=log2( )-1=-f(x),
)-1=-f(x),所以函数f(x)是奇函数.
(2)f(x)在区间(
 ,+∞)上的单调递减,证明如下
,+∞)上的单调递减,证明如下证明:令g(x)=
 =
= =
=
设
 ,则g(x1)-g(x2)=
,则g(x1)-g(x2)=

=
 =
=
∵
 ,则x1-x2<0,
,则x1-x2<0,
∴即g(x1)<g(x2)
∴g(x)在(
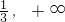 )上单调递减
)上单调递减由于y=log2g(x)在(0,+∞)单调递增,由复合函数的单调性可知y=
 在(
在(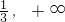 )单调递减
)单调递减分析:(1)由f(-x)=log2
 =log2
=log2 =log2(
=log2( )-1=-f(x),可得
)-1=-f(x),可得(2)令g(x)=
 =
= =
= ,只要利用单调性的定义先检验函数g(x)在(
,只要利用单调性的定义先检验函数g(x)在(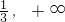 )上单调性,结合y=log2g(x)在(0,+∞)单调性及复合函数的单调性可判断
)上单调性,结合y=log2g(x)在(0,+∞)单调性及复合函数的单调性可判断点评:本题主要考查了奇偶函数的定义、函数单调性的定义在判断函数的奇偶性、单调性中中的应用,解题的关键是熟练掌握基本定义、基本方法

练习册系列答案
相关题目