题目内容
已知向量 =
= ,
, =
= =
= •
• +1.
+1.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)将函数y=f(x)的图象上所有点的纵坐标保持不变,横坐标缩短到原来的 倍;再把所得到的图象向左平移
倍;再把所得到的图象向左平移 个单位长度,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位长度,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的值域.
上的值域.
解:(1)f(x)= =
= =
=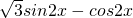 =2
=2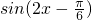 ,
,
∴函数f(x)的最小正周期T= =π,
=π,
由 ,解得
,解得 (k∈Z).
(k∈Z).
∴函数f(x)的单调递增区间为 (k∈Z);
(k∈Z);
(2)函数y=f(x)的图象上所有点的纵坐标保持不变,横坐标缩短到原来的 倍得到y=2
倍得到y=2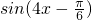 ,
,
再把所得到的图象向左平移 个单位长度,得到函数y=g(x)=2
个单位长度,得到函数y=g(x)=2 =2cos4x,
=2cos4x,
当x∈ 时,
时, ,
,
∴当x=0时,g(x)max=2;当 时,
时, =-1.
=-1.
∴函数y=g(x)在区间 上的值域为[-1,2].
上的值域为[-1,2].
分析:(1)利用数量积、两角和差的正弦公式即可把f(x)化为asin(ωx+φ)的形式,进而即可得出周期及其单调区间;
(2)利用图象变换的法则即可得到y=g(x),再利用三角函数的单调性即可得出值域.
点评:熟练掌握数量积、两角和差的正弦公式即可把f(x)化为asin(ωx+φ)的形式、三角函数周期及其单调性、图象变换的法则是解题的关键.
 =
= =
=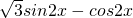 =2
=2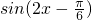 ,
,∴函数f(x)的最小正周期T=
 =π,
=π,由
 ,解得
,解得 (k∈Z).
(k∈Z).∴函数f(x)的单调递增区间为
 (k∈Z);
(k∈Z);(2)函数y=f(x)的图象上所有点的纵坐标保持不变,横坐标缩短到原来的
 倍得到y=2
倍得到y=2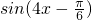 ,
,再把所得到的图象向左平移
 个单位长度,得到函数y=g(x)=2
个单位长度,得到函数y=g(x)=2 =2cos4x,
=2cos4x,当x∈
 时,
时, ,
,∴当x=0时,g(x)max=2;当
 时,
时, =-1.
=-1.∴函数y=g(x)在区间
 上的值域为[-1,2].
上的值域为[-1,2].分析:(1)利用数量积、两角和差的正弦公式即可把f(x)化为asin(ωx+φ)的形式,进而即可得出周期及其单调区间;
(2)利用图象变换的法则即可得到y=g(x),再利用三角函数的单调性即可得出值域.
点评:熟练掌握数量积、两角和差的正弦公式即可把f(x)化为asin(ωx+φ)的形式、三角函数周期及其单调性、图象变换的法则是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目