题目内容
以椭圆 的中心为顶点,左准线为准线的抛物线方程是 .
的中心为顶点,左准线为准线的抛物线方程是 .
【答案】分析:先求出椭圆  的左准线,即是抛物线的准线,再利用准线的方程与系数2p的关系求出p,即可求出抛物线方程.
的左准线,即是抛物线的准线,再利用准线的方程与系数2p的关系求出p,即可求出抛物线方程.
解答:解:因为椭圆 的
的
a=3,b= ,c=2,
,c=2,
∴椭圆的左准线为:x=-
所以 =
= ,2p=18且抛物线开口向右.
,2p=18且抛物线开口向右.
所以抛物线方程为y2=18x.
故答案为y2=18x.
点评:本题考查抛物线标准方程、椭圆的简单性质等基础知识,注意在求抛物线的标准方程时,一定要先判断出开口方向,再求方程.
 的左准线,即是抛物线的准线,再利用准线的方程与系数2p的关系求出p,即可求出抛物线方程.
的左准线,即是抛物线的准线,再利用准线的方程与系数2p的关系求出p,即可求出抛物线方程.解答:解:因为椭圆
 的
的a=3,b=
 ,c=2,
,c=2,∴椭圆的左准线为:x=-

所以
 =
= ,2p=18且抛物线开口向右.
,2p=18且抛物线开口向右.所以抛物线方程为y2=18x.
故答案为y2=18x.
点评:本题考查抛物线标准方程、椭圆的简单性质等基础知识,注意在求抛物线的标准方程时,一定要先判断出开口方向,再求方程.

练习册系列答案
相关题目
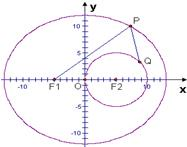 已知点P是椭圆
已知点P是椭圆 的中心为顶点,右焦点为焦点的抛物线方程是 .
的中心为顶点,右焦点为焦点的抛物线方程是 .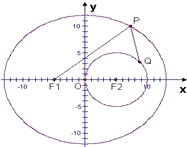 已知点P是椭圆
已知点P是椭圆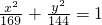 上一动点,点F1,F2是椭圆的左右两焦点.
上一动点,点F1,F2是椭圆的左右两焦点. 的中心为顶点,右焦点为焦点的抛物线方程是 .
的中心为顶点,右焦点为焦点的抛物线方程是 .