题目内容
设a、b是正实数，以下不等式：①
＞
；②a＞|a-b|-b；③a2+b2＞4ab-3b2；④ab+
＞2恒成立的序号为
- A.①③
- B.①④
- C.②③
- D.②④
D
分析：由a，b为正实数，对于①①利用基本不等式变形分析取值特点即可；对于②利用含绝对值不等式的性质即可加以判断；对于③取出反例数值即可；对于④利用均值不等式进行条件下的等价变形即可．
解答：∵a、b是正实数，
∴①a+b≥2?1≥
?≥．当且仅当a=b时取等号，∴①不恒成立；
②a+b＞|a-b|?a＞|a-b|-b恒成立；
③a2+b2-4ab+3b2=（a-2b）2≥0，当a=2b时，取等号，例如：a=1，b=2时，左边=5，右边=4×1×2-3×22=-4∴③不恒成立；
④ab+≥
=2
＞2恒成立．
答案：D
点评：此题考查了基本不等式，含绝对值不等式的性质，作差法比较多项式的大小．
分析：由a，b为正实数，对于①①利用基本不等式变形分析取值特点即可；对于②利用含绝对值不等式的性质即可加以判断；对于③取出反例数值即可；对于④利用均值不等式进行条件下的等价变形即可．
解答：∵a、b是正实数，
∴①a+b≥2
?1≥?≥．当且仅当a=b时取等号，∴①不恒成立；②a+b＞|a-b|?a＞|a-b|-b恒成立；
③a2+b2-4ab+3b2=（a-2b）2≥0，当a=2b时，取等号，例如：a=1，b=2时，左边=5，右边=4×1×2-3×22=-4∴③不恒成立；
④ab+
≥=2＞2恒成立．答案：D
点评：此题考查了基本不等式，含绝对值不等式的性质，作差法比较多项式的大小．
练习册系列答案
阅读快车系列答案
相关题目
（选做题）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分，解答时应写出文字说明、证明过程或演算步骤．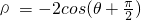
，
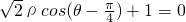，则曲线C1上的点与曲线C2上的点的最远距离为________．
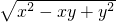，b=p
，c=x+y，若对任意的正实数x，y，都存在以a，b，c为三边长的三角形，则实数p的取值范围是________．
（t为参数），求直线l被曲线C截得的线段长度．
．
（t为参数），求直线l被曲线C截得的线段长度．
．
，
，则曲线C1上的点与曲线C2上的点的最远距离为 ．
，b=p
，c=x+y，若对任意的正实数x，y，都存在以a，b，c为三边长的三角形，则实数p的取值范围是 ．