题目内容
已知直线l1为曲线y=x2+x-2在P(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2.(Ⅰ)求直线l2的方程;
(Ⅱ)求由直线l1、l2和x轴所围成的三角形的面积.
解:(Ⅰ)y′=2x+1.直线l1的方程为:y=3x-3.
设直线l2过曲线y=x2+x-2上的点B(b,b2+b-2),
则l2的方程为y=(2b+1)x-b2-2.
因为l1⊥l2,则有2b+1=-![]() ,b=-
,b=-![]() .
.
所以直线l2的方程为y=-![]() x-
x-![]() .
.
(Ⅱ)解方程组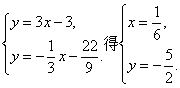
所以直线l1和l2的交点坐标为(![]() )
)
l1、l2与x轴交点的坐标分别为(1,0)、(![]() ,0).
,0).
所以所求三角形的面积S=![]()
温馨提示
要求与切线垂直的直线方程,关键是确定切线的斜率,从已知条件分析,求切线的斜率是可行的途径,可先通过求导确定曲线在点P处切线的斜率,再根据点斜式求出与切线垂直的直线方程.

练习册系列答案
相关题目