题目内容
高三年级有3名男生和1名女生为了报某所大学,事先进行了多方详细咨询,并根据自己的高考成绩情况,最终估计这3名男生报此所大学的概率都是 ,这1名女生报此所大学的概率是
,这1名女生报此所大学的概率是 .且这4人报此所大学互不影响。
.且这4人报此所大学互不影响。
(Ⅰ)求上述4名学生中报这所大学的人数中男生和女生人数相等的概率;
(Ⅱ)在报考某所大学的上述4名学生中,记 为报这所大学的男生和女生人数的和,试求
为报这所大学的男生和女生人数的和,试求 的分布列和数学期望.
的分布列和数学期望.
(1)
(2)ξ的公布列为:
∴E(ξ)=0×ξ 0 1 2 3 4 P 




 +1×
+1× +2×
+2× +3×
+3× +4×
+4× =
=
解析试题分析:解:(1)记“报这所大学的人数中男生和女生人数相等的”事件为A,男生人数记为Bi(i=0、1、2、3),女生人数记为Ci(i=0、1)
P(A)=P(B0C0)+P(B1C1)=

 =
= (5分)
(5分)
(2)ξ=0,1,2,3,4
P(ξ=0)=
P(ξ=1)=
 =
=
P(ξ=2)=
P(ξ=3)=
P(ξ=4)= (9分)
(9分)
∴ξ的公布列为:
∴E(ξ)=0×ξ 0 1 2 3 4 P 




 +1×
+1× +2×
+2× +3×
+3× +4×
+4× =
= (12分)
(12分)
考点:独立重复试验,以及分布列
点评:主要是考查了独立重复试验的概率公式的运用,以及分布列的求解和性质的运用,属于基础题。

下表是我国2010年和2011年2~6月CPI同比(即当年某月与前一年同月相比)的增长数据,其中2011年的5个CPI数据成等差数列.
(Ⅰ)求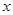 、
、 、
、 的值;
的值;
(Ⅱ)求2011年2~6月我国CPI数据的方差;
(Ⅲ)一般认为,某月CPI数据达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点为严重通货膨胀,现随机从2010年5个月和2011年5个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
我国2010年和2011年2~6月份的CPI数据(单位:百分点,1个百分点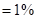 )
)
| 年份 | 二月 | 三月 | 四月 | 五月 | 六月 |
| 2010 | 2.7 | 2.4 | 2.8 | 3.1 | 3.9 |
| 2011 | 4.9 | 5.0 | 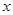 |  |  |
为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
⑴请将上面列连表补充完整,并判断是否有
 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望。
附:
 ,其中
,其中 
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 )获得身高数据的茎叶图如下:
)获得身高数据的茎叶图如下: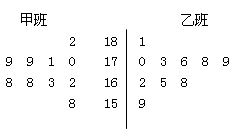
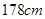 的同学,求至少有一名身高大于
的同学,求至少有一名身高大于 的同学被抽中的概率。
的同学被抽中的概率。 且各轮问题能否正确回答互不影响.
且各轮问题能否正确回答互不影响.  为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 ,审核过关后,甲、乙两人文化测试合格的概率分别为
,审核过关后,甲、乙两人文化测试合格的概率分别为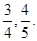
 表示甲,乙两人中获得自主招生入选资格的人数,求
表示甲,乙两人中获得自主招生入选资格的人数,求