题目内容
已知函数f(x)=2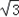 sinxcosx﹣2cos(x+
sinxcosx﹣2cos(x+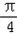 )cos(x﹣
)cos(x﹣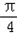 ).
).
(I)求函数f(x)的最小正周期和图象的对称轴方程;
(II)求函数f(x)在区间[﹣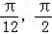 ]上的值域.
]上的值域.
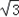 sinxcosx﹣2cos(x+
sinxcosx﹣2cos(x+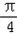 )cos(x﹣
)cos(x﹣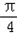 ).
).(I)求函数f(x)的最小正周期和图象的对称轴方程;
(II)求函数f(x)在区间[﹣
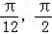 ]上的值域.
]上的值域.解:(I)求函数f(x)=2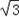 sinxcosx﹣2cos(x+
sinxcosx﹣2cos(x+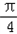 )cos(x﹣
)cos(x﹣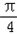 )
)
=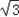 sin2x+sin(2x﹣
sin2x+sin(2x﹣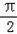 )=
)=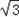 sin2x﹣cos2x=2sin(2x﹣
sin2x﹣cos2x=2sin(2x﹣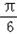 ).
).
故函数f(x)的最小正周期为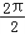 =π,
=π,
再由2x﹣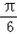 =kπ+
=kπ+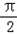
可得对称轴方程为 x=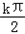 +
+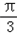 ,k∈z.
,k∈z.
(II)∵﹣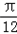 ≤x≤
≤x≤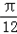 ,
,
∴﹣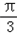 ≤2x﹣
≤2x﹣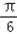 ≤
≤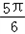 ,
,
故当 2x﹣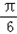 =
=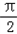 时,函数取得最大值为2,
时,函数取得最大值为2,
当 2x﹣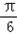 =﹣
=﹣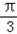 时,函数取得最小值为﹣2
时,函数取得最小值为﹣2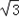 ×
× =﹣
=﹣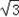 ,
,
故函数f(x)在区间[﹣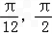 ]上的值域为[﹣
]上的值域为[﹣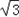 ,2].
,2].
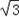 sinxcosx﹣2cos(x+
sinxcosx﹣2cos(x+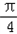 )cos(x﹣
)cos(x﹣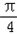 )
)=
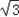 sin2x+sin(2x﹣
sin2x+sin(2x﹣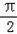 )=
)=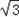 sin2x﹣cos2x=2sin(2x﹣
sin2x﹣cos2x=2sin(2x﹣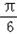 ).
).故函数f(x)的最小正周期为
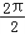 =π,
=π,再由2x﹣
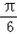 =kπ+
=kπ+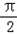
可得对称轴方程为 x=
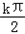 +
+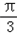 ,k∈z.
,k∈z.(II)∵﹣
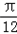 ≤x≤
≤x≤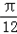 ,
,∴﹣
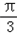 ≤2x﹣
≤2x﹣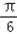 ≤
≤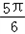 ,
,故当 2x﹣
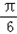 =
=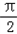 时,函数取得最大值为2,
时,函数取得最大值为2,当 2x﹣
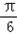 =﹣
=﹣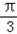 时,函数取得最小值为﹣2
时,函数取得最小值为﹣2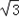 ×
× =﹣
=﹣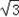 ,
,故函数f(x)在区间[﹣
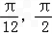 ]上的值域为[﹣
]上的值域为[﹣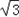 ,2].
,2].
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目