Question

（理）（改编题）

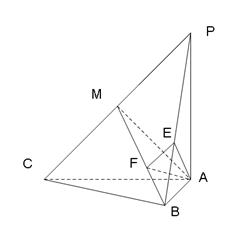
如图，三棱锥中，，．

（Ⅰ）求证：平面；

（Ⅱ）若为线段上的点，设，问为何值时能使

直线平面；（只理科做）

（Ⅲ）求二面角的大小． 

                                                                                             

Answer 1

,

解析:

（Ⅰ） ，

∴ ，，

 ，

∴ 平面．                         　                 ……………………2分

（Ⅱ）当M为PC中点时，即时，直线平面，　　  ……3分

证明如下：

由（Ⅰ）知平面，平面，∴ ，　在等腰中， M为中点，∴ ， 又，

∴ 平面．                                　  ………6分

（Ⅲ）

由(Ⅱ)知当M为PC中点时，平面， 平面，

∴ 平面平面．                         ………7分

过作于，∴ 平面                                                         

作于，连结，由三垂线定理可知，．

∴ 为二面角的平面角．         ………9分

设，则．

在中，，

由(Ⅰ)知平面，平面，∴ ．

在中，．

由面积公式得,,             ………10分

同理，在中，由面积公式得，………11分

在中，．

所以二面角的大小为．        ……………12分

方法二：

(Ⅰ)同方法一．                                       　     …………………3分

(Ⅱ)如图，以A为坐标原点，所在直线分别为轴，轴，轴建立空间直角坐标系．                      

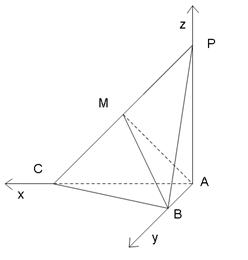
设，则，  　  ……………4分

当M为PC中点时，即时，直线平面．    …………5分

证明如下：

当M为PC中点时，．

，,．

,                    

∴ ，即．                          …………6分

，            

∴ ，即．                           …………7分

又，∴ 平面．               ………8分

（Ⅲ）可证平面．                                   

则平面法向量为，                               

下面求平面PBC的法向量．

设平面PBC的法向量为，

,，

，

令，则，                      　   ……………10分

．

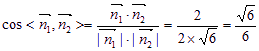所以二面角的大小为．           …………12分