题目内容
已知函数f(x)=(x2﹣a)ex.
(1)若a=3,求f(x)的单调区间和极值;
(2)若x1,x2为f(x)的两个不同的极值点,且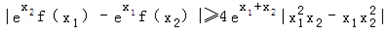 ,
,
若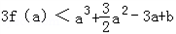 恒成立,求实数b的取值范围.
恒成立,求实数b的取值范围.
解(1)∵a=3,∴f(x)=(x2﹣3)ex,
f'(x)=(x2+2x﹣3)ex=0
∴x=﹣3或x=1
令f'(x)>0,解得x∈(﹣∞,﹣3)∪(1,+∞)
令f'(x)<0,解得x∈(﹣3,1),
∴f(x)的递增区间为(﹣∞,﹣3)∪(1,+∞);
递减区间为(﹣3,1)
当x=﹣3时,函数有极大值为6e﹣3,当x=1时函数有极小值为﹣2e;
(2)由(x)=(x2+2x﹣a)ex=0可得x2+2x﹣a=0
由题意两根为x1,x2,
∴x1+x2=﹣2,x1x2=﹣a,
又∵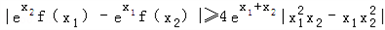 ,
,
∴| |≥4
|≥4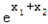 |
|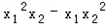 |
|
∴|x1+x2|≥4|x1x2|
∴﹣ ≤a≤
≤a≤ 且△=4+4a>0,
且△=4+4a>0,
∴﹣ ≤a≤
≤a≤
设g(a)=3f(a)﹣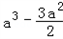 +3a=3(a2﹣a)ea﹣
+3a=3(a2﹣a)ea﹣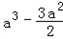 +3a
+3a
∴g'(a)=3(a2+a﹣1)(ea﹣1)=0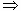 a=
a=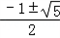 或a=0
或a=0
又∵﹣ ≤a≤
≤a≤ 函数在[﹣
函数在[﹣ ,0)上单调递增,在[0,
,0)上单调递增,在[0, ]上单调递减
]上单调递减
∴g(a)max=g(0)=0
∴b>0
f'(x)=(x2+2x﹣3)ex=0
∴x=﹣3或x=1
令f'(x)>0,解得x∈(﹣∞,﹣3)∪(1,+∞)
令f'(x)<0,解得x∈(﹣3,1),
∴f(x)的递增区间为(﹣∞,﹣3)∪(1,+∞);
递减区间为(﹣3,1)
当x=﹣3时,函数有极大值为6e﹣3,当x=1时函数有极小值为﹣2e;
(2)由(x)=(x2+2x﹣a)ex=0可得x2+2x﹣a=0
由题意两根为x1,x2,
∴x1+x2=﹣2,x1x2=﹣a,
又∵
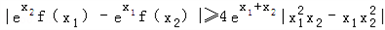 ,
,∴|
 |≥4
|≥4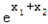 |
|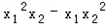 |
|∴|x1+x2|≥4|x1x2|
∴﹣
 ≤a≤
≤a≤ 且△=4+4a>0,
且△=4+4a>0,∴﹣
 ≤a≤
≤a≤
设g(a)=3f(a)﹣
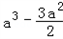 +3a=3(a2﹣a)ea﹣
+3a=3(a2﹣a)ea﹣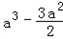 +3a
+3a∴g'(a)=3(a2+a﹣1)(ea﹣1)=0
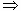 a=
a=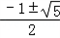 或a=0
或a=0又∵﹣
 ≤a≤
≤a≤ 函数在[﹣
函数在[﹣ ,0)上单调递增,在[0,
,0)上单调递增,在[0, ]上单调递减
]上单调递减∴g(a)max=g(0)=0
∴b>0

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|