题目内容
函数f(x)=2x2-1nx的递增区间是________.

分析:先求出函数f(x)=2x2-1nx的导数,再令导数大于0,即可求得函数f(x)=2x2-1nx的递增区间
解答:由题,函数的定义域是(0,+∞)
∵f(x)=2x2-1nx
∴f′(x)=4x-

令f′(x)>0,即4x-
 >0
>0解得x>
 或x<-
或x<-
又函数的定义域是(0,+∞)
∴函数f(x)=2x2-1nx的递增区间是
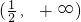
故答案为
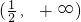
点评:本题利用导数研究函数的单调性,解题的关键是理解并掌握函数的导数的符号与函数的单调性的关系,此类题一般有两类题型,一类是利用导数符号得出单调性,一类是由单调性得出导数的符号,本题属于第一种类型根据导数求单调区间.

练习册系列答案
相关题目
函数f(x)=2x2-6x+1在区间[-1,1]上的最小值为( )
| A、9 | ||
| B、-3 | ||
C、
| ||
D、
|