题目内容
设A={1,2,3,4,5,6},则满足条件f(f(x))=f(x)的映射f:A→A的个数为
- A.66
- B.720
- C.960
- D.1057
D
分析:由f[f(x)]=f(x)可知集合A={1,2,3,4,5,6}的像f(A)(即所有f(x)构成的集合)在映射f下保持不变,即对于任意x∈f(A)总有f(x)=x,则问题转化为对f(A)的讨论,根据组合数直接写出各种情况的映射的个数,最后求和即可.
解答:由f[f(x)]=f(x)可知集合A={1,2,3,4,5,6}的像f(A)(即所有f(x)构成的集合)在映射f下保持不变,即对于任意x∈f(A)总有f(x)=x,则问题转化为对f(A)的讨论:
(1)f(A)中有6个元素时,只能为f(1)=1,f(2)=2,f(3)=3,f(4)=4,f(5)=5,f(6)=6.共1种.
(2)f(A)中有5个元素时,比如f(A)={1,2,3,4,5},只能为f(1)=1,f(2)=2,f(3)=3,f(4)=4,f(5)=5,f(6)=1,2,3,4,5,共 ×5=30种.
×5=30种.
(3)f(A)中有4个元素时,比如f(A)={1,2,3,4},只能为f(1)=1,f(2)=2,f(3)=3,f(4)=4,f(5)=1,2,3,4,f(6)=1,2,3,4,共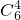 ×42=240种.
×42=240种.
(4)f(A)中有3个元素时,同理 ×33=540种.
×33=540种.
(5)f(A)中有2个元素时,同理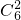 ×24=240种.
×24=240种.
(6)f(A)中有1个元素时,同理 ×1=6种.
×1=6种.
共1057种.
故选D.
点评:本题考查了映射、排列、组合及简单计数问题知识,由于形式比较我,所以可分类讨论就能做出答案.
分析:由f[f(x)]=f(x)可知集合A={1,2,3,4,5,6}的像f(A)(即所有f(x)构成的集合)在映射f下保持不变,即对于任意x∈f(A)总有f(x)=x,则问题转化为对f(A)的讨论,根据组合数直接写出各种情况的映射的个数,最后求和即可.
解答:由f[f(x)]=f(x)可知集合A={1,2,3,4,5,6}的像f(A)(即所有f(x)构成的集合)在映射f下保持不变,即对于任意x∈f(A)总有f(x)=x,则问题转化为对f(A)的讨论:
(1)f(A)中有6个元素时,只能为f(1)=1,f(2)=2,f(3)=3,f(4)=4,f(5)=5,f(6)=6.共1种.
(2)f(A)中有5个元素时,比如f(A)={1,2,3,4,5},只能为f(1)=1,f(2)=2,f(3)=3,f(4)=4,f(5)=5,f(6)=1,2,3,4,5,共
 ×5=30种.
×5=30种.(3)f(A)中有4个元素时,比如f(A)={1,2,3,4},只能为f(1)=1,f(2)=2,f(3)=3,f(4)=4,f(5)=1,2,3,4,f(6)=1,2,3,4,共
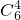 ×42=240种.
×42=240种.(4)f(A)中有3个元素时,同理
 ×33=540种.
×33=540种.(5)f(A)中有2个元素时,同理
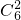 ×24=240种.
×24=240种.(6)f(A)中有1个元素时,同理
 ×1=6种.
×1=6种.共1057种.
故选D.
点评:本题考查了映射、排列、组合及简单计数问题知识,由于形式比较我,所以可分类讨论就能做出答案.

练习册系列答案
相关题目
设a∈{1,2,3,4},b∈{2,4,8,12},则函数f(x)=x3+ax-b在区间[1,2]上有零点的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|