题目内容
20.在△ABC中,a,b,c分别为角A,B,C所对的边,且ccosA=b,则△ABC是( )| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 斜三角形 |
分析 根据正弦定理结合题中的等式,化简得sinCcosA=sinB,再用sin(A+C)=sinB展开化简得到cosCsinA=0,结合三角形内角的范围即可得到C=$\frac{π}{2}$,即△ABC是直角三角形.
解答 解:∵在△ABC中,ccosA=b,
∴根据正弦定理,得sinCcosA=sinB,…①
∵A+C=π-B,
∴sin(A+C)=sinB,即sinB=sinCcosA+cosCsinA,
将①代入,可得cosCsinA=0,
∵A、C∈(0,π),可得sinA>0,
∴cosC=0,得C=$\frac{π}{2}$,即△ABC是直角三角形,
故选:C.
点评 本题给出三角形的边角关系,判断三角形的形状,着重考查了两角和的正弦公式和正弦定理等知识,属于基础题.

练习册系列答案
相关题目
8.过椭圆 $\frac{x^2}{16}$+$\frac{y^2}{9}$=1的右焦点F2作直线l交椭圆于A、B两点,F1是椭圆的左焦点,则△AF1B 的周长为( )
| A. | 20 | B. | 16 | C. | 12 | D. | 10 |
12.已知等比数列{an}的公比为正数,且a3•a9=2a52,a2=2,则a1的值是( )
| A. | $±\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
9.执行如图所示的程序框图,若输出i的值是11,则判断框中的横线上可以填入的最大整数为( )
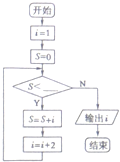

| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
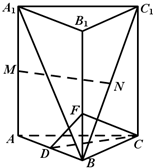 如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.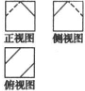 一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{24}$.
一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{24}$.