题目内容
甲乙丙3位同学选修课程,从4门课程中选。甲选修2门,乙丙各选修3门,则不同的选修方案共有
| A.36种 | B.48种 | C.96种 | D.1 92种 |
C
解析试题分析:设4门课程分别为1,2,3,4,甲选修2门,可有1,2;1,3;1,4;2,3;2,4;3,4共6种情况,同理乙,丙均可有1,2,3;1,2,4;2,3,4;1,3,4共4种情况,∴不同的选修方案共有6×4×4=96种,故选C.
考点:分步计数原理
点评:本题需注意方案不分次序,即a,b和b,a是同一种方案,用列举法找到相应的组合即可.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
从6人中选4人分别到北京、哈尔滨、广州、成都四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且在这6人中甲、乙不去哈尔滨游览,则不同的选择方案共有
| A.300种 | B.240种 | C.144种 | D.96种 |
4名同学到某景点旅游,该景点有4条路线可供游览,其中恰有1条路线没有被这4个同学中的任何1人游览的情况有
| A.36种 | B.72种 | C.81种 | D.144种 |
从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有一人参加,星期六有两人参加,星期日有一人参加,则不同的选派方法共有( )
| A.120种 | B.96种 | C.60种 | D.48种 |
若 ,则
,则 等于( )
等于( )
| A.1 | B.-1 | C.10 | D.0 |
2013年第12届全国运动会举行期间,某校4名大学生申请当A,B,C三个比赛项目的志愿者,组委会接受了他们的申请,每个比赛项目至少分配一人,每人只能服务一个比赛项目,若甲要求不去服务A比赛项目,则不同的安排方案共有( )
| A.20种 | B.24种 | C.30种 | D.36种 |
设(x-b) =b
=b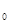 +b
+b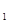 x+b
x+b x
x +…+b
+…+b x
x ,如果b
,如果b +b
+b =-6,则实数b的值为
=-6,则实数b的值为
A. | B.- | C.2 | D.-2 |
二项式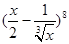 的展开式中常数项是
的展开式中常数项是
| A.28 | B.-7 | C.7 | D.-28 |