题目内容
对任意正整数x、y都有f(x+y)=f(x)•f(y),且 ,则f(1)+f(2)+…+f(2008)=
,则f(1)+f(2)+…+f(2008)=
- A.1-
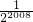
- B.

- C.

- D.

A
分析:对任意正整数x,y都有f(x+y)=f(x)•f(y),且 ,可得f(n)=f(n-1)•f(1)=
,可得f(n)=f(n-1)•f(1)= ,从而可得f(1)+f(2)+…+f(2008)=
,从而可得f(1)+f(2)+…+f(2008)= ,利用等比数列的求和公式可求
,利用等比数列的求和公式可求
解答:对任意正整数x,y都有f(x+y)=f(x)•f(y),且 f(1)= ,
,
∴f(2)=f(1).f(1)= ,
, ,,…f(n)=f(n-1)•f(1)=
,,…f(n)=f(n-1)•f(1)=
∴f(1)+f(2)+…+f(2008)=
= =
=
故选A.
点评:本题主要考查了等比数列求和的公式的应用,解题得关键是要根据题中的已知条件中的递推公式求解出f(n)得通项公式.
分析:对任意正整数x,y都有f(x+y)=f(x)•f(y),且
 ,可得f(n)=f(n-1)•f(1)=
,可得f(n)=f(n-1)•f(1)= ,从而可得f(1)+f(2)+…+f(2008)=
,从而可得f(1)+f(2)+…+f(2008)= ,利用等比数列的求和公式可求
,利用等比数列的求和公式可求解答:对任意正整数x,y都有f(x+y)=f(x)•f(y),且 f(1)=
 ,
,∴f(2)=f(1).f(1)=
 ,
, ,,…f(n)=f(n-1)•f(1)=
,,…f(n)=f(n-1)•f(1)=
∴f(1)+f(2)+…+f(2008)=

=
 =
=
故选A.
点评:本题主要考查了等比数列求和的公式的应用,解题得关键是要根据题中的已知条件中的递推公式求解出f(n)得通项公式.

练习册系列答案
相关题目
对任意正整数x,y都有f(x+y)=f(x)•f(y),且f(1)=
,则f(1)+f(2)+…+f(2011)=( )
| 1 |
| 2 |
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、
|
 ,则
,则 [f(1)+f(2)+f(3)+…+f(n)]=( )
[f(1)+f(2)+f(3)+…+f(n)]=( )


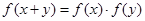 ,且
,且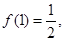 则
则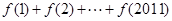 =
(
)
=
(
)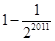 B.
B.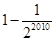 C.
C. D.
D. 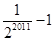 [来源:]
[来源:]