题目内容
2.下列数列中个数均为正数,且各行依次成等差数列,各列依次成等比数列,公比均相等,已知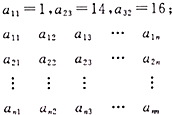
(1)求数列{an1}的通项公式;
(2)设bn=$\frac{{a}_{1n}}{{a}_{n1}}$,n∈N+,Tn为数列{bn}的前n项和,若Tn<m2-7m对一切n∈N+都成立,求最小的正整数m的值.
分析 (1)设第一行等差数列的公差为d,等比数列的公比为q,(q>0),由题意得到关于d,q的方程组解之得到通项公式;
(2)由(1)得到数列bn的通项公式,利用错位相减法求和,然后根据恒成立问题求m的值.
解答 解:(1)设第一行等差数列的公差为d,等比数列的公比为q,(q>0),由题意得$\left\{\begin{array}{l}{(1+2d)q=14}\\{(1+d){q}^{2}=16}\end{array}\right.$,解答d=3,q=2,∴an1=a11•qn-1=2n-1;
(2)由(1)得a1n=a11+(n-1)d=3n-2,∴bn=$\frac{3n-2}{{2}^{n-1}}$,
∴Tn=$\frac{1}{{2}^{0}}+\frac{4}{{2}^{1}}+\frac{7}{{2}^{2}}+…+\frac{3n-5}{{2}^{n-2}}+\frac{3n-2}{{2}^{n-1}}$,
$\frac{1}{2}{T}_{n}=\frac{1}{2}+\frac{4}{{2}^{2}}+\frac{7}{{2}^{3}}+…+\frac{3n-5}{{2}^{n-1}}+\frac{3n-2}{{2}^{n}}$,
∴$\frac{1}{2}{T}_{n}$=1+3×($\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n-1}}$)-$\frac{3n-2}{{2}^{n}}$=1+3×$\frac{\frac{1}{2}[1-(\frac{1}{2})^{n-1}]}{1-\frac{1}{2}}$-$\frac{3n-2}{{2}^{n}}$=4-$\frac{3}{{2}^{n-1}}-\frac{3n-2}{{2}^{n}}$.
所以Tn=8-$\frac{3n+4}{{2}^{n-1}}$,又Tn<m2-7m对一切n∈N+都成立,故m2-7m>(Tn)max,n∈N+,
所以m2-7m≥8,即m≥8或m≤-1,所以最小的正整数m的值是8.
点评 本题考查了数列的通项公式、数列求和以及恒成立问题的解答;关键是由题意求出数列的通项公式,利用错位相减法求和.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案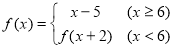 ,则
,则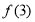 为
为