题目内容
已知函数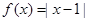
(1)解不等式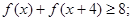
(2)若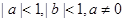 .求证:
.求证: .
.
(1) ;(2)证明过程详见解析.
;(2)证明过程详见解析.
解析试题分析:本题主要考查绝对值不等式的解法和证明不等式问题,考查分类讨论思想和转化能力以及计算能力.第一问,用零点分段法去掉绝对值,解不等式组;第二问,用作差法证明不等式,通过平方去掉绝对值,比较大小.
试题解析:(Ⅰ) ,
,
当 时,由
时,由 ,解得
,解得 ;
;
当 时,
时, 不成立;
不成立;
当 时,由
时,由 ,解得
,解得 . 4分
. 4分
所以不等式 的解集为
的解集为 . 5分
. 5分
(Ⅱ) ,即
,即 . 6分
. 6分
因为 ,
, ,所以
,所以 ,
,
所以 .故所证不等式成立. 10分
.故所证不等式成立. 10分
考点:1.绝对值不等式的解法;2.作差法证明不等式.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
若不等式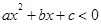 的解集为{x| x<-
的解集为{x| x<-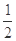 或x>
或x>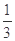 },则
},则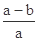 的值为 ( )
的值为 ( )
A.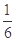 | B.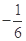 | C.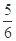 | D.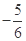 |
 ,
, ,且
,且 ,则
,则 的最小值为________.
的最小值为________. >
> ;④a>b⇒ac2>bc2;⑤
;④a>b⇒ac2>bc2;⑤ >
> ⇒a>b.其中真命题的序号是_______.
⇒a>b.其中真命题的序号是_______. ,
, ,
, .
.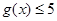 时,恒有
时,恒有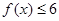 ,求
,求 的最大值;
的最大值; 时,恒有
时,恒有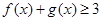 ,求
,求 、
、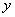 是不全为零的实数,试比较
是不全为零的实数,试比较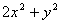 与
与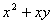 的大小;
的大小;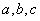 为正数,且
为正数,且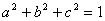 ,求证:
,求证: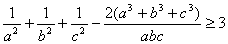 .
.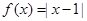 .
.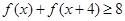 ;
;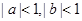 ,且
,且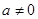 ,求证:
,求证: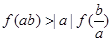 .
. 都是正数,且
都是正数,且
 与
与 的大小.
的大小.