题目内容
函数f（x）=x3-x2+mx在R内是增函数，则m的取值范围为________．
[
，+∞）
分析：函数f（x）=x3-x2+mx在R内是增函数，则恒有f′（x）≥0，由此即可求得a的范围．
解答：f′（x）=3x2-2x+m．
因为函数f（x）=x3-x2+mx在R内是增函数，所以f′（x）=3x2-2x+m≥0在R上恒成立，
故有△=4-12m≤0，即m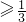
．
所以m的取值范围为[，+∞）．
故答案为[，+∞）
点评：本题考查导数与函数单调性的关系，属基础题，难度不大．可导函数f（x）在某区间上单调递增的充要条件是f′（x）≥0（不恒为0）．
，+∞）分析：函数f（x）=x3-x2+mx在R内是增函数，则恒有f′（x）≥0，由此即可求得a的范围．
解答：f′（x）=3x2-2x+m．
因为函数f（x）=x3-x2+mx在R内是增函数，所以f′（x）=3x2-2x+m≥0在R上恒成立，
故有△=4-12m≤0，即m
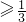．所以m的取值范围为[
，+∞）．故答案为[
，+∞）点评：本题考查导数与函数单调性的关系，属基础题，难度不大．可导函数f（x）在某区间上单调递增的充要条件是f′（x）≥0（不恒为0）．
练习册系列答案
科学实验活动册系列答案
相关题目