题目内容
18.已知双曲线$\frac{x^2}{12}-\frac{y^2}{4}=1$的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线的斜率的取值范围是( )| A. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | B. | $\left?{-\sqrt{3},\sqrt{3}}\right?$ | C. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | D. | $({-\sqrt{3},\sqrt{3}})$ |
分析 渐近线方程y=$±\frac{\sqrt{3}}{3}$x,当过焦点的两条直线与两条渐近线平行时,这两条直线与双曲线右支分别只有一个交点,由此能求出此直线的斜率的取值范围.
解答 解:渐近线方程y=$±\frac{\sqrt{3}}{3}$x,
当过焦点的两条直线与两条渐近线平行时,
这两条直线与双曲线右支分别只有一个交点
(因为双曲线正在与渐近线无限接近中),
那么在斜率是[$-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}$]两条直线之间的所有直线中,
都与双曲线右支只有一个交点.
此直线的斜率的取值范围[$-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}$].
故选:A.
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到直线与双曲线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
8.曲线${∫}_{-\sqrt{2}}^{2}$(-$\sqrt{2-{x}^{2}}$)dx( )
| A. | -2π | B. | -π | C. | 2π | D. | π |
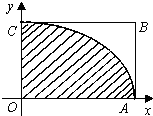 如图,曲线AC的方程为$\frac{x^2}{9}+\frac{y^2}{4}$═1(0≤x≤3,0≤y≤2),为估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积,现采用随机模拟方式产生x∈(0,3),y∈(0,2)的200个点(x,y),经统计,落在图中阴影部分的点共157个,则可估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积是18.84.(精确到0.01)
如图,曲线AC的方程为$\frac{x^2}{9}+\frac{y^2}{4}$═1(0≤x≤3,0≤y≤2),为估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积,现采用随机模拟方式产生x∈(0,3),y∈(0,2)的200个点(x,y),经统计,落在图中阴影部分的点共157个,则可估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积是18.84.(精确到0.01)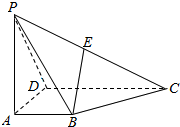 如图所示,四棱锥P-ABCD的底面是一梯形,AB∥CD,CD=3AB,过点B作平面PAD的平行线交直线PC于点E,则点PE:EC=1:2.
如图所示,四棱锥P-ABCD的底面是一梯形,AB∥CD,CD=3AB,过点B作平面PAD的平行线交直线PC于点E,则点PE:EC=1:2.