题目内容
已知函数f（x）的定义域为（-∞，0）∪（0，+∞）且对定义域中任意x均有：f（x）•f（-x）=1，
g（x）=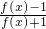
，则g（x）
- A.是奇函数
- B.是偶函数
- C.既是奇函数又是偶函数
- D.既非奇函数又非偶函数
A
分析：由题意先判断函数g（x）的定义域关于原点对称，再求出g（-x）与g（x）的关系，判断出其奇偶性．
解答：由题意，要使函数g（x）有意义，则f（x）+1≠0，即f（x）≠-1，
∵对定义域中任意x均有：f（x）•f（-x）=1，
∴若f（a）=-1时，则有f（-a）=-1，
∵函数f（x）的定义域为（-∞，0）∪（0，+∞），
∴函数g（x）的定义域也关于原点对称，
∵g（-x）=
=
=-=-g（x），
∴函数g（x）是奇函数．
故选A．
点评：本题考查了函数的奇偶性的判断方法，即先求函数的定义域判断是否关于原点对称，再利用奇函数和偶函数的定义进行验证，易忽视是求函数的定义域．
分析：由题意先判断函数g（x）的定义域关于原点对称，再求出g（-x）与g（x）的关系，判断出其奇偶性．
解答：由题意，要使函数g（x）有意义，则f（x）+1≠0，即f（x）≠-1，
∵对定义域中任意x均有：f（x）•f（-x）=1，
∴若f（a）=-1时，则有f（-a）=-1，
∵函数f（x）的定义域为（-∞，0）∪（0，+∞），
∴函数g（x）的定义域也关于原点对称，
∵g（-x）=
==-=-g（x），∴函数g（x）是奇函数．
故选A．
点评：本题考查了函数的奇偶性的判断方法，即先求函数的定义域判断是否关于原点对称，再利用奇函数和偶函数的定义进行验证，易忽视是求函数的定义域．
练习册系列答案
相关题目
