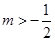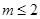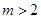题目内容
已知函数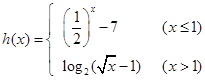
(1)判断函数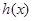 在区间
在区间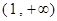 上的单调性并用定义证明;
上的单调性并用定义证明;
(2)若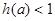 ,求
,求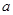 的取值范围.
的取值范围.
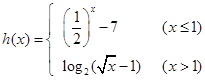
(1)判断函数
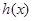 在区间
在区间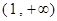 上的单调性并用定义证明;
上的单调性并用定义证明;(2)若
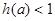 ,求
,求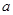 的取值范围.
的取值范围.(1) 时,
时, ,则
,则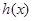 在区间
在区间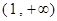 上为增函数
上为增函数
(2)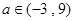
 时,
时, ,则
,则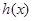 在区间
在区间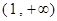 上为增函数
上为增函数(2)
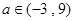
本试题主要是考查了函数单调性的定义的运用,利用定义证明函数的单调性以及进行求解含有参数的不等式的综合运用问题。
(1)先判定结论,然后设变量,比较大小,从而说明结论。
(2)利用参数a的范围
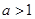 和
和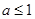 来分类讨论,求解得到。
来分类讨论,求解得到。
解:(1)当 时,
时, ,则
,则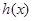 在区间
在区间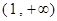 上为增函数
上为增函数
任取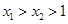 ,
,

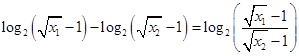 ---------------4分
---------------4分
由幂函数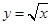 在
在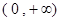 上为增函数可知
上为增函数可知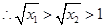 ,
,
即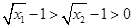 ,则
,则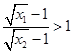 ,
,

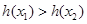 ,
,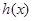 在区间
在区间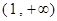 上为增函数.--------- -----6分
上为增函数.--------- -----6分
(2)若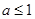 ,则
,则 ,即
,即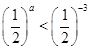

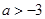 ,则
,则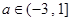 --------------8 分
--------------8 分
若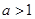 ,则
,则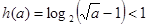 ,即
,即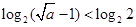 ,
,

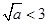 ,即
,即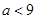 ,则
,则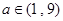 综上所述,
综上所述,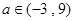
(1)先判定结论,然后设变量,比较大小,从而说明结论。
(2)利用参数a的范围
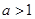 和
和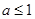 来分类讨论,求解得到。
来分类讨论,求解得到。解:(1)当
 时,
时, ,则
,则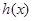 在区间
在区间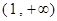 上为增函数
上为增函数任取
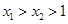 ,
,
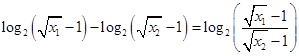 ---------------4分
---------------4分由幂函数
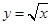 在
在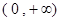 上为增函数可知
上为增函数可知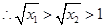 ,
,即
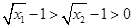 ,则
,则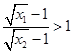 ,
,

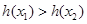 ,
,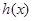 在区间
在区间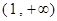 上为增函数.--------- -----6分
上为增函数.--------- -----6分(2)若
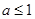 ,则
,则 ,即
,即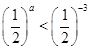

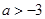 ,则
,则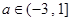 --------------8 分
--------------8 分 若
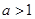 ,则
,则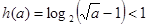 ,即
,即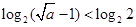 ,
,
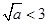 ,即
,即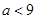 ,则
,则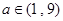 综上所述,
综上所述,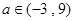

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
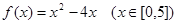 的最大值与最小值可以得其值域为 ( )
的最大值与最小值可以得其值域为 ( )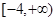
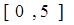
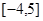
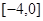
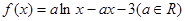 .
.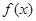 的单调区间;
的单调区间;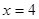 处切线的斜率为
处切线的斜率为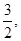 若函数
若函数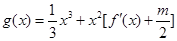 在区间(1,3)上不是单调函数,求m的取值范围.
在区间(1,3)上不是单调函数,求m的取值范围.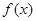 是定义在
是定义在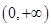 上的增函数,则不等式
上的增函数,则不等式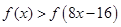 的解集是( )
的解集是( )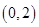
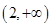
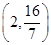
 满足:①定义在
满足:①定义在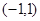 上;②当
上;②当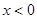 时,
时,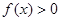 ;③对于任意的
;③对于任意的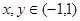 ,有
,有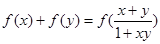 .
.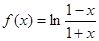 ,验证它是否满足条件②,③;
,验证它是否满足条件②,③; 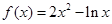 的递增区间是 ( )
的递增区间是 ( )
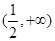
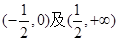
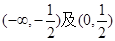
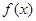 在定义域R内可导,若
在定义域R内可导,若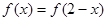 ,且当
,且当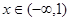 时,
时,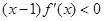 .设
.设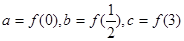 ,则( )
,则( )
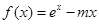 的图像为曲线C,若曲线C不存在与直线
的图像为曲线C,若曲线C不存在与直线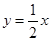 垂直的切线,则实数m的取值范围是( )
垂直的切线,则实数m的取值范围是( )