Question

已知点A（-1，1），B（1，1），点P是直线y=x-2上的一点，满足∠APB最大，求点P的坐标及∠APB的最大值.

Answer 1

思路解析：设出P点坐标，可分别求出直线PA、PB的斜率，根据到角公式计算.

解：设P（t，t-2），则k_AP=，k_BP=，

当t=3时，∠APB=0；当t=1时，P（1，-1），BP∥Oy，AB∥Ox，

∴AB⊥PB且|AB|=|PB|=2，∠APB=；

当t＜3且t≠1时,tan∠APB==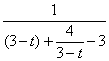≤1,

当且仅当3-t=,即t=1或t=5时等号成立,而t＜3且t≠1,

∴tan∠APB＜1,即∠APB＜;

当t＞3时,同法可求∠APB的最大值是arctan＜.

综上所述,当P点的坐标是(1,-1)时,∠APB有最大值.