题目内容
设Sn为等差数列{an}的前n项和,若a1=1,公差d=2,Sk+2-Sk=24,则k=________.
5
分析:先由等差数列前n项和公式求得Sk+2,Sk,将Sk+2-Sk=24转化为关于k的方程求解.
解答:根据题意:Sn =na1 +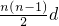 =n2.
=n2.
∴Sk+2=(k+2)2,Sk=k2.
∴Sk+2-Sk=24转化为:(k+2)2-k2=24,∴k=5.
故答案为:5.
点评:本题主要考查等差数列的前n项和公式及其应用,得到Sn =n2,是解题的关键,同时还考查了方程思想,属中档题.
分析:先由等差数列前n项和公式求得Sk+2,Sk,将Sk+2-Sk=24转化为关于k的方程求解.
解答:根据题意:Sn =na1 +
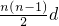 =n2.
=n2.∴Sk+2=(k+2)2,Sk=k2.
∴Sk+2-Sk=24转化为:(k+2)2-k2=24,∴k=5.
故答案为:5.
点评:本题主要考查等差数列的前n项和公式及其应用,得到Sn =n2,是解题的关键,同时还考查了方程思想,属中档题.

练习册系列答案
相关题目
设Sn为等差数列{an}的前n项和,若S8=30,S4=7,则a4的值等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|