题目内容
已知双曲线 的准线过椭圆
的准线过椭圆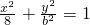 的焦点,则直线y=kx+3与椭圆至少有一个交点的充要条件为
的焦点,则直线y=kx+3与椭圆至少有一个交点的充要条件为
- A.k∈(-∞,
 ,+∞)
,+∞) - B.
 ,
,
- C.k∈(-∞,
 ,+∞)
,+∞) - D.
 ,
,
A
分析:写出双曲线的准线得到椭圆的焦点,得到b的值,写出椭圆的标准方程,联立直线与椭圆的方程,得到关于x的一元二次方程,根据直线y=kx+3与椭圆至少有一个交点,得到△≥0,求出结果.
解答:双曲线 的准线为
的准线为 ,
,
椭圆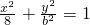 的半焦距
的半焦距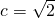 ,于是8=b2+2,
,于是8=b2+2,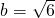 ,
,
所以椭圆方程为 .
.
联立方程,得
消y得:3x2+4(kx+3)2=24,
整理得(3+4k2)x2+24kx+12=0,
要使直线y=kx+3与椭圆至少有一个交点,则有△≥0.
即:(24k)2-4×(3+4k2)×12≥0,12k2-3-4k2≥0, ,
, 或
或 .
.
故选A.
点评:本题考查双曲线的几何性质和直线与椭圆的交点个数问题,本题解题的关键是写出椭圆的标准方程,方程联立,根据一元二次方程的根的判别式得到结果.
分析:写出双曲线的准线得到椭圆的焦点,得到b的值,写出椭圆的标准方程,联立直线与椭圆的方程,得到关于x的一元二次方程,根据直线y=kx+3与椭圆至少有一个交点,得到△≥0,求出结果.
解答:双曲线
 的准线为
的准线为 ,
,椭圆
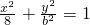 的半焦距
的半焦距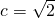 ,于是8=b2+2,
,于是8=b2+2,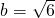 ,
,所以椭圆方程为
 .
.联立方程,得

消y得:3x2+4(kx+3)2=24,
整理得(3+4k2)x2+24kx+12=0,
要使直线y=kx+3与椭圆至少有一个交点,则有△≥0.
即:(24k)2-4×(3+4k2)×12≥0,12k2-3-4k2≥0,
 ,
, 或
或 .
.故选A.
点评:本题考查双曲线的几何性质和直线与椭圆的交点个数问题,本题解题的关键是写出椭圆的标准方程,方程联立,根据一元二次方程的根的判别式得到结果.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 C.
C.  D.
D. 
 D.
D. 
 D.
D. 
 的准线过椭圆
的准线过椭圆 的焦点,则直线
的焦点,则直线 与
与 B.
B.
 D.
D.
 的准线过椭圆
的准线过椭圆 的焦点,则直线
的焦点,则直线 与椭圆至多有一个交点的充要条件是( )
与椭圆至多有一个交点的充要条件是( ) B.
B.
 D.
D.