题目内容
已知函数 ,
, .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若 在区间
在区间 上是减函数,求
上是减函数,求 的取值范围.
的取值范围.
(1) ;(2)
;(2) 或
或
解析试题分析:(1)当 时,
时, ,可通过求函数
,可通过求函数 的导数,从面得到切线的斜率,然后由点斜式写出直线的方程;
的导数,从面得到切线的斜率,然后由点斜式写出直线的方程;
(2)可先求出 ,则由
,则由 在区间
在区间 上是减函数可知
上是减函数可知 在区间
在区间 上恒成立,可通过解不等式组
上恒成立,可通过解不等式组 获解.
获解.
试题解析:解:(1)
(2) ,然后对
,然后对 进行分类讨论的
进行分类讨论的 或
或
考点:1、导数的几何意义;2、导数在研究函数性质中的应用.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 (其中
(其中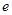 为自然对数的底数).
为自然对数的底数).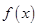 的单调区间;
的单调区间;  在区间
在区间 上的取值范围为
上的取值范围为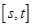 ,则称区间
,则称区间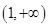 上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.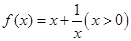 ,以点
,以点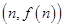 为切点作函数图像的切线
为切点作函数图像的切线 ,直线
,直线 与函数
与函数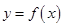 图像及切线
图像及切线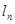 分别相交于
分别相交于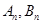 ,记
,记 .
.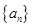 的通项;
的通项;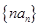 的前
的前 项和为
项和为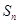 ,求证:
,求证: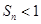 .
.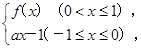 且g(x)≤1恒成立,求实数a的取值范围.
且g(x)≤1恒成立,求实数a的取值范围. +ln x-1.
+ln x-1. ,
, ,
, .
. ,设函数
,设函数 ,求
,求 的极大值;
的极大值; ,讨论
,讨论 的单调性.
的单调性.