题目内容
选修4-5:不等式选讲
关于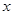 的不等式
的不等式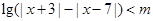 .
.
(1)当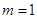 时,解此不等式;
时,解此不等式;
(2)设函数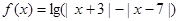 ,当
,当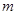 为何值时,
为何值时,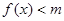 恒成立?
恒成立?
关于
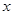 的不等式
的不等式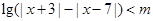 .
.(1)当
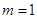 时,解此不等式;
时,解此不等式;(2)设函数
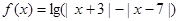 ,当
,当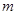 为何值时,
为何值时,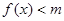 恒成立?
恒成立?(1) ;(2)即
;(2)即 时,
时,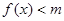 恒成立.
恒成立.
 ;(2)即
;(2)即 时,
时,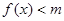 恒成立.
恒成立.本试题主要是考查了绝对值不等式的求解,以及运用对数函数的单调性,并能结合对数函数的性质,求解不等式的恒成立问题。这类问题常常转化为求解最值问题来得到参数的取值范围。
解:(1)当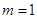 时,原不等式可变为
时,原不等式可变为 ,
,
可得其解集为 ……………………..(4分)
……………………..(4分)
(2)设 , …………………..(5分)
, …………………..(5分)
则由对数定义及绝对值的几何意义知 , ……………………….(7分)
, ……………………….(7分)
因 在
在 上为增函数,
上为增函数,
则 ,当
,当 时,
时, , ……………(9分)
, ……………(9分)
故只需 即可,
即可,
即 时,
时,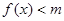 恒成立. ……………..(10分)
恒成立. ……………..(10分)
解:(1)当
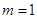 时,原不等式可变为
时,原不等式可变为 ,
,可得其解集为
 ……………………..(4分)
……………………..(4分)(2)设
 , …………………..(5分)
, …………………..(5分)则由对数定义及绝对值的几何意义知
 , ……………………….(7分)
, ……………………….(7分)因
 在
在 上为增函数,
上为增函数, 则
 ,当
,当 时,
时, , ……………(9分)
, ……………(9分)故只需
 即可,
即可,即
 时,
时,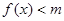 恒成立. ……………..(10分)
恒成立. ……………..(10分)

练习册系列答案
相关题目

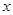 的不等式
的不等式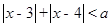 ,
,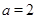 时解不等式;
时解不等式; 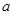 的范围.
的范围. 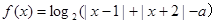 .
.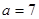 时,求函数
时,求函数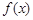 的定义域;
的定义域;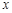 的不等式
的不等式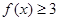 的解集是
的解集是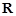 ,求实数
,求实数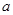 的取值范围.
的取值范围. 的解集为
的解集为 ,则实数
,则实数 __________.
__________.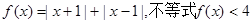 的解集为M。
的解集为M。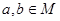 时,证明:
时,证明: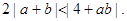
 ,若不等式
,若不等式 对任意实数
对任意实数 恒成立,则
恒成立,则 取值集合是_______________________.
取值集合是_______________________.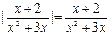 的解集是 ( )
的解集是 ( )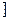
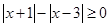 的解集是______.
的解集是______.