题目内容
已知二次函数f(x)满足:
(1)若f(x+1)=2x+f(x),f(0)=1,求f(x)的解析式;
(2)若f(2-x)=f(2+x),f(x)最大值为5,f(0)=1,求f(x)的解析式.
解:(1)设f(x)=ax2+bx+c(a≠0)(1分)
∵f(0)=1∴c=1(2分)
∵f(x+1)=2x+f(x)
∴a(x+1)2+b(x+1)+1=2x+ax2+bx+(13分)
整理,得2ax+a+b=2x(4分)
∴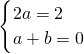 (5分)
(5分)
∴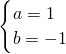 (6分)
(6分)
∴f(x)=x2-x+(17分)
(2)由f(2-x)=f(2+x),得f(x)对称轴是x=2(8分)
设f(x)=a(x-2)2+5(10分)
由f(0)=1,得a×(0-2)2+5=1∴a=-1(12分)
∴f(x)=-(x-2)2+5.(13分)
分析:(1)用待定系数法设f(x)=ax2+bx+c(a≠0)f(0)=1?c=1,再利用两方程相等对应项系数相等来求a,b.
(2)f(2-x)=f(2+x)?对称轴是x=2,再有f(x)最大值为5,设f(x)=a(x-2)2+5利用f(0)=1求出a即可.
点评:本题考查了二次函数解析式的求法.二次函数解析式的确定,应视具体问题,灵活的选用其形式,再根据题设条件列方程组,即运用待定系数法来求解.在具体问题中,常常会与图象的平移,对称,函数的周期性,奇偶性等知识有机的结合在一起.
∵f(0)=1∴c=1(2分)
∵f(x+1)=2x+f(x)
∴a(x+1)2+b(x+1)+1=2x+ax2+bx+(13分)
整理,得2ax+a+b=2x(4分)
∴
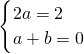 (5分)
(5分)∴
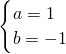 (6分)
(6分)∴f(x)=x2-x+(17分)
(2)由f(2-x)=f(2+x),得f(x)对称轴是x=2(8分)
设f(x)=a(x-2)2+5(10分)
由f(0)=1,得a×(0-2)2+5=1∴a=-1(12分)
∴f(x)=-(x-2)2+5.(13分)
分析:(1)用待定系数法设f(x)=ax2+bx+c(a≠0)f(0)=1?c=1,再利用两方程相等对应项系数相等来求a,b.
(2)f(2-x)=f(2+x)?对称轴是x=2,再有f(x)最大值为5,设f(x)=a(x-2)2+5利用f(0)=1求出a即可.
点评:本题考查了二次函数解析式的求法.二次函数解析式的确定,应视具体问题,灵活的选用其形式,再根据题设条件列方程组,即运用待定系数法来求解.在具体问题中,常常会与图象的平移,对称,函数的周期性,奇偶性等知识有机的结合在一起.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目