题目内容
 现在小型轿车慢慢进入百姓家庭,但是另一个问题相继暴露出来--堵车.李先生居住在城市的A处,准备开车到B处上班,若该地各路段发生堵车事件是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图所示(例如A→C→D并作两个路段:路段AC发生堵车事件的概率是
现在小型轿车慢慢进入百姓家庭,但是另一个问题相继暴露出来--堵车.李先生居住在城市的A处,准备开车到B处上班,若该地各路段发生堵车事件是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图所示(例如A→C→D并作两个路段:路段AC发生堵车事件的概率是| 1 |
| 10 |
| 1 |
| 15 |
(1)请你为李先生选择一条由A到B的路线,使得沿途经过的路口尽可能少,且发生堵车的概率最小;
(2)若该路线A→C→F→B中遇到堵车的次数为随机变量X,求X的数学期望.
分析:(1)分别求出路线A→C→D→B遇到堵车的概率,路线A→C→F→B遇到堵车的概率,路线A→E→F→B遇到堵车的概率,即得到发生堵车的概率最小的路线;
(2)由题意知路线A→C→F→B中遇到堵车次数X可取值为0,1,2,3.结合变量对应的事件,写出变量的分布列和期望.
(2)由题意知路线A→C→F→B中遇到堵车次数X可取值为0,1,2,3.结合变量对应的事件,写出变量的分布列和期望.
解答:解:(1)设在路段AC堵车的事件为 G,在路段CD堵车的事件为H,在路段DB堵车的事件为J,
则路线A→C→D→B遇到堵车的概率是:P=1-P(
•
•
)=1-P(
)P(
)P(
)=
1-[1-P(G)][1-P(H)][1-P(J)]=1-
×
×
=
同理:路线A→C→F→B遇到堵车的概率是
,
路线A→E→F→B遇到堵车的概率是
,
所以应选择线路A→E→F→B可使途中发生堵车的概率最小.
(2)路线A→C→F→B中遇到堵车的次数 X取值可能是 0,1,2,3,
所以P(X=0)=(1-
)(1-
)(1-
)=
=
,
P(X=1)=(
)(1-
)(1-
)+(1-
)(
)(1-
)+(1-
)(1-
)(
)=
,
P(X=2)=(
)(
)(1-
)+(1-
)(
)(
)+(
)(1-
)(
)=
,
P(X=3)=
•
•
=
故 X的分布列为
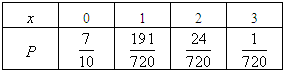
所以EX=0×
+1×
+2×
+3×
=
=
.
则路线A→C→D→B遇到堵车的概率是:P=1-P(
. |
| G |
. |
| H |
. |
| J |
. |
| G |
. |
| H |
. |
| J |
1-[1-P(G)][1-P(H)][1-P(J)]=1-
| 9 |
| 10 |
| 14 |
| 15 |
| 5 |
| 6 |
| 3 |
| 10 |
同理:路线A→C→F→B遇到堵车的概率是
| 3 |
| 10 |
路线A→E→F→B遇到堵车的概率是
| 89 |
| 320 |
所以应选择线路A→E→F→B可使途中发生堵车的概率最小.
(2)路线A→C→F→B中遇到堵车的次数 X取值可能是 0,1,2,3,
所以P(X=0)=(1-
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 504 |
| 720 |
| 7 |
| 10 |
P(X=1)=(
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 191 |
| 720 |
P(X=2)=(
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 24 |
| 720 |
P(X=3)=
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 8 |
| 1 |
| 720 |
故 X的分布列为

所以EX=0×
| 7 |
| 10 |
| 191 |
| 720 |
| 24 |
| 720 |
| 1 |
| 720 |
| 242 |
| 720 |
| 121 |
| 360 |
点评:本题考查离散型随机变量的分布列和期望问题,考查相互独立事件同时发生的概率,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难.

练习册系列答案
相关题目