题目内容
直线
过抛物线
的焦点，且与抛物线交于
、
两点，若线段
的长是8，的中点到
轴的距离是2，则此抛物线方程是
A． | B． | C． | D． |
B
解析
练习册系列答案
相关题目
F1，F2是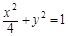
的左、右焦点，点P在椭圆上运动，则
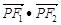的最大值是
| A．4 | B．5 | C．2 | D．1 |
的焦点为
、
，
为双曲线上一点，
，则双曲线的离心率（ ）
.已知
是抛物线
上一个动点，
是椭圆
上的一个动点，定点
.若
轴，且
，则
的周长
的取值范围是( )
A． | B． | C． | D． |
已知
为两定点，
为
的一条切线，若过
的抛物线以直线为准线，则抛物线的焦点所在的轨迹是（）
| A．双曲线 | B．椭圆 | C．抛物线 | D．圆 |
设M（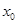
，
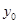）为抛物线C：
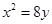上一点，F为抛物线C的焦点，以F为圆心、
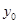为半径的圆和抛物线C的准线相交，则的取值范围是 （ ）
| A．（0，2） | B．[0，2] | C．（2，+∞） | D．[2，+∞） |
P是椭圆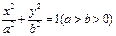
上的点,
是椭圆的焦点,若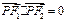
且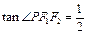
. 则此椭圆的离心率为（ ）
A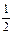． | B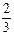． | C． | D． |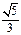
我们把离心率为黄金比
的椭圆称为“优美椭圆”．设
(a>b>0)
为“优美椭圆”，F、A分别是它的左焦点和右顶点，B是它短轴的一个端点，则∠ABF等于
| A．60° | B．75° | C．90° | D．120° |