题目内容
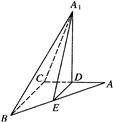 在Rt△ABC中,AC=4,BC=3,∠C=90°,D,E分别为AC,AB边上的点,且DE∥BC,沿DE将△ADE折起(记为△A1DE),使二面角A1-DE-B为直二面角.
在Rt△ABC中,AC=4,BC=3,∠C=90°,D,E分别为AC,AB边上的点,且DE∥BC,沿DE将△ADE折起(记为△A1DE),使二面角A1-DE-B为直二面角.(1)当E点在何处时,A1B的长度最小,并求出最小值;
(2)当A1B的长度最小时,求二面角A1-BE-C的大小.
分析:(1)由已知,,∠CDA1为二面角A1-DE-B的平面角,∠CDA1=90°,设CD=x,表示出A1B,建立函数关系,求函数的最值即可.
(2)过D 作DH⊥AE于H,则可得∠A1HD是二面角A1-BE-C的平面角,在直角△A1HD中求解.
(2)过D 作DH⊥AE于H,则可得∠A1HD是二面角A1-BE-C的平面角,在直角△A1HD中求解.
解答:解:(1)∵DE∥BC,∴CD⊥DE,A1D⊥DE,∴∠CDA1为二面角A1-DE-B的平面角,,∴∠CDA1=90°
设CD=x,AD=4-x,则A1B2=BC2+CD2+DA12=2x2-8x+25=2(x-2)2+17
当x=2时,即D为CA中点,此时EBA为中点时,AB有最小值
(2)过D 作DH⊥AE于H,∵A1D⊥ABC 连接A1H∴A1H⊥AE
∴∠A1HD是二面角A1-BE-C的平面角
tan∠A1HD=
=
=
,∴∠A1HD=arctan
.
二面角A1-BE-C的大小为arctan
.
设CD=x,AD=4-x,则A1B2=BC2+CD2+DA12=2x2-8x+25=2(x-2)2+17
当x=2时,即D为CA中点,此时EBA为中点时,AB有最小值
| 17 |
(2)过D 作DH⊥AE于H,∵A1D⊥ABC 连接A1H∴A1H⊥AE
∴∠A1HD是二面角A1-BE-C的平面角
tan∠A1HD=
| A1D |
| DH |
| 2 | ||
|
| 5 |
| 3 |
| 5 |
| 3 |
二面角A1-BE-C的大小为arctan
| 5 |
| 3 |
点评:本题考查二面角的定义、计算,空间距离的计算,二次函数的性质,以及建模解模的数学能力.

练习册系列答案
相关题目
在Rt△ABC中,∠A=90°,|
|=1,则
•
的值为:( )
| AB |
| AB |
| BC |
| A、1 | B、-1 |
| C、1或-1 | D、不能确定 |
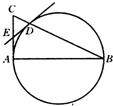 15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.