题目内容
如图,在四棱锥 中,
中, ,
, ,
,
 平面
平面 ,
, 为
为 的中点,
的中点, .
.
( I ) 求证: ∥平面
∥平面 ;
;
( II ) 求四面体 的体积.
的体积.
 |
1)
法一: 取AD得中点M,连接EM,CM.
则EM//PA
 因为
因为
所以, (2分)
(2分)
在 中,
中,
所以,
而 ,所以,MC//AB. (3分)
,所以,MC//AB. (3分)
因为
所以, (4分)
(4分)
 又因为
又因为
所以,
因为 (6分)
(6分)
法二: 延长DC,AB,交于N点,连接PN.
因为
所以,C为ND的中点. (3分)
因为E为PD的中点
所以,EC//PN
因为
 (6分)
(6分)
2)
法一:由已知条件有;AC=2AB=2,AD=2AC=4,CD= (7分)
(7分)
因为,
所以, (8分)
(8分)
又因为
所以,  (10分)
(10分)
因为E是PD的中点
所以点E平面PAC的距离

所以,四面体PACE的体积 (12分)
(12分)
法二:由已知条件有;AC=2AB=2,AD=2AC=4,CD=
因为,
所以, (10分)
(10分)
因为E是PD的中点
所以,四面体PACE的体积 (12分)
(12分)

练习册系列答案
相关题目
 ,若函数
,若函数 有大于零的极值点,则m的取值范围是
有大于零的极值点,则m的取值范围是 ,则目标函数
,则目标函数 的最小值为 .
的最小值为 . ,则下列结论正确的是
,则下列结论正确的是 的图像关于直线
的图像关于直线 对称 B.
对称 B.  对称
对称 D.
D.  上为增函数
上为增函数 为锐角,且
为锐角,且 ,则
,则 .
. ,且
,且 ,则
,则 ( )
( ) B、
B、 C、
C、 D、
D、
 的左右两支上各有一点
的左右两支上各有一点 ,点
,点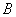 在直线
在直线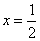 上的射影是点
上的射影是点 ,若直线
,若直线 过右焦点,则直线
过右焦点,则直线 必过点( )
必过点( ) B、
B、 C、
C、 D、
D、
 上单调递增的函数是( )
上单调递增的函数是( ) B.
B. C.
C. D.
D.
 ,则使函数
,则使函数 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有 的值有( )
的值有( )