题目内容
设等差数列{ }的前n项和为
}的前n项和为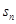 ,已知
,已知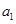 =-2012,
=-2012, =2,则
=2,则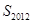 =( )
=( )
| A.-2013 | B.2013 | C.-2012 | D.2012 |
C
解析试题分析:
 就是前2013项的平均数,即
就是前2013项的平均数,即 ,同理,
,同理,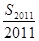 =
=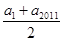 ,两式相减得
,两式相减得 ,
,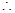 d=2,最后
d=2,最后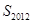 =2012
=2012 +
+ =2012x(-2012)+2012x2011=-2012
=2012x(-2012)+2012x2011=-2012
考点:等差数列的性质

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等比数列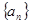 中,各项都是正数,且
中,各项都是正数,且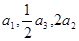 成等差数列,则
成等差数列,则 等于 ( )
等于 ( )
A.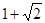 | B.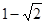 | C. | D.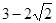 |
数列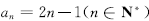 排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )
排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )
| A.61 | B.62 | C.63 | D.64 |
已知等差数列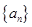 的公差
的公差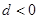 ,若
,若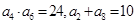 ,则该数列的前
,则该数列的前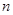 项和
项和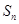 的最大值是( )
的最大值是( )
A.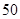 | B.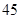 | C.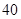 | D.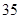 |
正项等比数列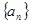 满足
满足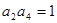 ,
,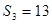 ,
, ,则数列
,则数列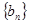 的前10项和是( ).
的前10项和是( ).
| A.65 | B.-65 | C.25 | D.-25 |
已知 为等差数列,若
为等差数列,若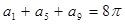 ,则
,则 的值为( )
的值为( )
A.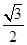 | B. | C.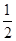 | D.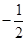 |
已知数列{ }是公差为3的等差数列,且
}是公差为3的等差数列,且 成等比数列,则
成等比数列,则 等于( )
等于( )
| A.30 | B.27 | C.24 | D.33 |
等差数列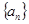 的前
的前 项和为
项和为 ,公差为
,公差为 ,已知
,已知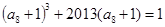 ,
,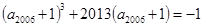 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. | B.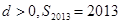 |
C.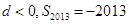 | D.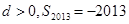 |
等差数列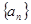 的公差
的公差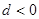 ,且
,且 ,则该数列的前
,则该数列的前 项和取得最大值时,
项和取得最大值时,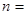
| A.6 | B.7 | C.6或7 | D.7或8 |