题目内容
人造地球卫星的运行轨道是以地心为一个焦点的椭圆.设地球半径为R,卫星近地点、远地点离地面的距离分别是r1,r2,则卫星轨道的离心率=
.
| r2-r1 |
| 2R+r1+r2 |
| r2-r1 |
| 2R+r1+r2 |
分析:由题意画出图形,结合椭圆的定义,求出椭圆的长半轴a,半焦距c,即可确定椭圆的离心率.
解答: 解:椭圆的离心率:e=
解:椭圆的离心率:e=
∈(0,1),(c,半焦距;a,长半轴)
所以只要求出椭圆的c和a,
由题意,结合图形可知,
a=
,
c=OF1=
-r1-R=
,
所以e=
=
=
.
故答案为:
.
 解:椭圆的离心率:e=
解:椭圆的离心率:e=| c |
| a |
所以只要求出椭圆的c和a,
由题意,结合图形可知,
a=
| r1+r2+2R |
| 2 |
c=OF1=
| r1+r2+2R |
| 2 |
| r2-r1 |
| 2 |
所以e=
| c |
| a |
| ||
|
| r2-r1 |
| 2R+r1+r2 |
故答案为:
| r2-r1 |
| 2R+r1+r2 |
点评:本题是基础题,考查椭圆的离心率的求法,注意半焦距与长半轴的求法,是解题的关键,考查学生的作图视图能力.

练习册系列答案
相关题目
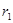 ,
, ,则卫星轨道的离心率为 .
,则卫星轨道的离心率为 .