题目内容
正方体ABCD—A1B1C1D1的边长为4,M、N、E、F分别是A1D1、A1B1、D1C1、B1C1的中点.(1)求证:平面AMN∥平面EFBD;
(2)求平面AMN与平面EFBD间的距离.
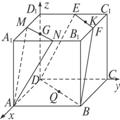
(1)证明:如图,建立坐标系,则A(4,0,0),M(2,0,4),N(4,2,4),D(0,0,0),B(4,4,0),E(0,2,4),F(2,4,4).
取MN之中点G及EF之中点K,BD之中点Q,则G(3,1,4),K(1,3,4),Q(2,2,0).
∴![]() =(2,2,0),
=(2,2,0),![]() =(2,2,0),
=(2,2,0),![]() =(-1,1,4),
=(-1,1,4),![]() =(-1,1,4).
=(-1,1,4).
可见![]() =
=![]() ,
,![]() =
=![]() ,
,
∴MN∥EF,AG∥QK,
∴MN∥平面EFBD,AG∥平面EFBD,
∴平面AMN∥平面EFBD.
(2)解:设n=(1,λ,μ)是平面EFBD的法向量,
则n·![]() =(1,λ,μ)·(2,2,0)=2+2λ=0,
=(1,λ,μ)·(2,2,0)=2+2λ=0,
及n·![]() =(1,λ,μ)·(-1,1,4)=-1+λ+4μ=0,
=(1,λ,μ)·(-1,1,4)=-1+λ+4μ=0,
∴λ=-1,μ=![]() ,∴n=(1,-1,
,∴n=(1,-1,![]() ).
).
两平面之间的距离为
d=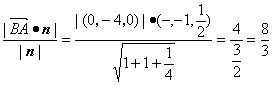 .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的: 已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点. 如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.
如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积. 如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )
如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )