Question

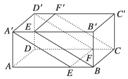
如图所示，在长方体ABCD-A₁B₁C₁D₁中，AB=AD=1，AA₁=2，M是棱CC₁的中点．
（1）求异面直线A₁M和C₁D₁所成的角的正切值；
（2）求BM与平面A₁B₁M所成的角大小．

Answer 1

分析：（1）由长方体的几何特征，可得∠MA₁B₁为异面直线A₁M与C₁D₁所成的角，解△MA₁B₁即可得到异面直线A₁M和C₁D₁所成的角的正切值；
（2）由长方体的几何特征可得A₁B₁⊥平面BCC₁B₁，进而由线面垂直的定义可得A₁B₁⊥BM，结合（1）中结论及勾股定理可得BM⊥B₁M，进而由线面垂直的判定定理可得BM⊥平面A₁B₁M，即BM与面A₁B₁M成90度角．

解答：解：（1）如图，因为C₁D₁∥B₁A₁，
所以∠MA₁B₁为异面直线A₁M与C₁D₁所成的角．
因为A₁B₁⊥平面BCC₁B₁，所以∠A₁B₁M=90°，
而A₁B₁=1，B₁M=

2

，故tan∠MA₁B₁=

B1M

A1B1

=

2

．
即异面直线A₁M和C₁D₁所成的角的正切值为

2

．
（2）由A₁B₁⊥平面BCC₁B₁，BM?平面平面BCC₁B₁，得
A₁B₁⊥BM①
由（1）知，B₁M=

2

，
又BM=

BC2+CM2

=

2

，B₁B=2，
所以B₁M²+BM²=B₁B²，从而BM⊥B₁M②
又A₁B₁∩B₁M=B₁，
∴BM⊥平面A₁B₁M，
∴BM与面A₁B₁M成90度角．

点评：本题考查的知识点是异面直线及其所成的角，直线与平面所成的角，其中利用平移法，将异面直线夹角转化为解三角形问题是解答（1）的关键，而熟练掌握线面垂直的判定定理是解答（2）的关键．