题目内容
【题目】已知函数f（x）=sin2x+2 
sin（x+ 
）cos（x﹣ ）﹣cos2x﹣ ．
（1）求函数f（x）的单调递减区间；
（2）求函数f（x）在[﹣ 
， 
π]上的最大值．
【答案】
（1）解：∵函数f（x）=sin2x+2 
sin（x+ 
）cos（x﹣ ）﹣cos2x﹣
=﹣cos2x+2 （ 
sinx+ cosx）（ cosx+ sinx）﹣ =﹣cos2x+2 （ 
+ sin2x）﹣
= sin2x﹣cos2x=2sin（2x﹣ 
），
令2kπ+ 
≤2x﹣ ≤2kπ+ 
，求得kπ+ 
≤x≤kπ 
，可得函数的减区间为[kπ+ ，kπ ]，k∈Z
（2）解：在[﹣ 
， 
π]上，2x﹣ ∈[﹣ 
， 
]，故当2x﹣ = 时，函数f（x）取得最大值为2
【解析】（1）利用三角恒等变换化简函数的解析式，再利用正弦函数的单调性求得函数的减区间．（2）利用正弦函数的定义域和值域，求得函数f（x）在[﹣ ， π]上的最大值．
【考点精析】本题主要考查了正弦函数的单调性和三角函数的最值的相关知识点，需要掌握正弦函数的单调性：在
上是增函数；在
上是减函数；函数
，当
时，取得最小值为
；当
时，取得最大值为
，则
，
，
才能正确解答此题．
练习册系列答案
相关题目
【题目】随着生活水平的提高，越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣，下图为其等高条形图：
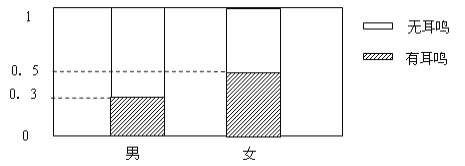
绘出2×2列联表；
②根据列联表的独立性检验，能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系？
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
附：
