题目内容

椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别是F1，F2，过F2作倾斜角为120°的直线与椭圆的一个交点为M，若MF1垂直于MF2，则椭圆的离心率为（　　）
分析：结合图形，根据Rt△MF2 F1中，在Rt△MF1F2中，F1F2=2c，∠F1F2M=60°，求出MF2，MF1
根据椭圆的定义列出关于a、c的方程，求
c
a
的值．
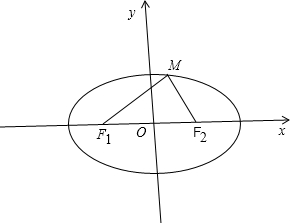解答：解：如图，
在Rt△MF1F2中，F1F2=2c，
∵∠F1F2M=60°，
∴MF2=c，MF1=2c×
3
2
=
3
c
MF1+MF2=c+
3
c=2a，⇒e=
c
a
=
2
3
+1
=
3
-1，
故选B．
点评：本题考查直角三角形中的边角关系，椭圆的简单性质，一元二次方程的解法．
练习册系列答案
相关题目
已知椭圆
x2
a2
+
y2
b
=1(a＞b＞0)的左、右焦点分别为F1、F2，离心率e=
2
2
，右准线方程为x=2．
（1）求椭圆的标准方程；
（2）过点F1的直线l与该椭圆交于M、N两点，且|
F2M
+
F2N
|=
2
26
3
，求直线l的方程．
精英家教网如图，椭圆
x2
a2
+
y2
b 
=1（a＞b＞0）与过点A（2，0）B（0，1）的直线有且只有一个公共点T，且椭圆的离心率e=
3
2
．
（Ⅰ）求椭圆方程；
（Ⅱ）设F1、F2分别为椭圆的左、右焦点，求证：|AT|2=
1
2
|AF1||AF2|．
精英家教网如图，椭圆
x2
a2
+
y2
b 
=1（a＞b＞0）与过点A（2，0）B（0，1）的直线有且只有一个公共点T，且椭圆的离心率e=
3
2
．
（Ⅰ）求椭圆方程；
（Ⅱ）设F1、F2分别为椭圆的左、右焦点，M为线段AF1的中点，求证：∠ATM=∠AF1T．
设 A（x1，y1）、B（x2，y2）是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上的两点，O为坐标原点，向量
m
=(
x1
a
，
y1
b
)，
n
=(
x2
a
，
y2
b
)且
m
•
n
=0．
（1）若A点坐标为（a，0），求点B的坐标；
（2）设
OM
=cosθ•
OA
+sinθ•
OB
，证明点M在椭圆上；
（3）若点P、Q为椭圆 上的两点，且
PQ
∥
OB
，试问：线段PQ能否被直线OA平分？若能平分，请加以证明；若不能平分，请说明理由．
已知椭圆
x2
a2
+
y2
b
=1(a＞b＞0)的左、右焦点分别为F1、F2，离心率e=
2
2
，右准线方程为x=2．
（1）求椭圆的标准方程；
（2）过点F1的直线l与该椭圆交于M、N两点，且|
F2M
+
F2N
|=
2
26
3
，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网