Question

已知椭圆的一个焦点为F(2,0),对应准线为x=3,离心率e=.

       (1)求椭圆的方程;

       (2)椭圆上是否存在两点A、B,与直线y=x上两点C、D构成矩形ABCD,使其面积取最大值?若存在,求直线AB的方程;若不存在,请说明理由.

      

Answer 1

解析:(1)设P(x,　y)为椭圆上的任一点,?

       由题意得,?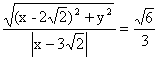

       化简得=1.?

       (2)假设A、B存在,设直线AB的方程为y=x+b,?

       则A、B两点的坐标是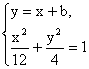的解,?

       消去y得4x²+6bx+3b²-12=0,(*)?

       x₁+x₂=-b,x₁x₂=.?

       ∴|x₁-x₂|²=(x₁+x₂)²-4x₁x₂=12-b².?

       ∴|AB|=.?

       直线AB与y=x的距离d=|b|.?

       ∴矩形ABCD的面积为S=|AB|·d=·|b|?

       =.?

       ∴当b²=8,即b=±2时,S取最大值.?

       又∵b=±2时(*)的Δ=36b²-16(3b²-12)=96>0,?

       ∴满足条件的A、B存在,直线AB的方程为y=x±2.